Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Watson, G. L.
1978.
One‐class genera of positive quadratic forms in nine and ten variables.
Mathematika,
Vol. 25,
Issue. 1,
p.
57.
Cassels, J.W.S.
1982.
Proceedings of the International Mathematical Conference.
Vol. 74,
Issue. ,
p.
9.
Jagy, William C.
Kaplansky, Irving
and
Schiemann, Alexander
1997.
There are 913 regular ternary forms.
Mathematika,
Vol. 44,
Issue. 2,
p.
332.
Lorch, David
and
Kirschmer, Markus
2013.
Single-class genera of positive integral lattices.
LMS Journal of Computation and Mathematics,
Vol. 16,
Issue. ,
p.
172.
Gao, Lei
and
Qin, Hourong
2019.
Ternary quadratic forms and the class numbers of imaginary quadratic fields.
Communications in Algebra,
Vol. 47,
Issue. 11,
p.
4605.


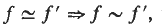 , where
, where 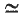 denote equivalence and semi-equivalence respectively. Trivially, it suffices to find the primitive
denote equivalence and semi-equivalence respectively. Trivially, it suffices to find the primitive 