Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T19:18:47.909Z Has data issue: false hasContentIssue false
  • English
  • Français

On the union of convex bodies with no interior point in common

Part of: General convexity

Published online by Cambridge University Press:  26 February 2010

P. R. Scott
P. R. Scott
Affiliation:
Department of Pure Mathematics, University of Adelaide, Adelaide, SA 5001, South Australia.
Get access

Extract

Let K1, K2,…, Kd+1 be d+1 convex bodies in Ed, the interiors of which have no point in common. If mX denotes the measure of set X, we prove

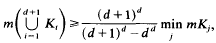
and this inequality is best possible.

MSC classification

Secondary: 52A20: Convex sets in $n$ dimensions (including convex hypersurfaces)
Type
Research Article
Information
Mathematika , Volume 37 , Issue 2 , December 1990 , pp. 245 - 250
Copyright
Copyright © University College London 1990

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Eggleston, H. G.. Convexity. Cambridge Tract No. 47 (Cambridge University Press, 1963).Google Scholar
2. Grünbaum, B.. Partitions of mass-distributions and of convex bodies by hyperplanes. Pacific J. Math., 10 (1960), 1257–1261.CrossRefGoogle Scholar
3. Scott, P. R.. On three sets with no point in common. Mathematika, 25 (1978), 17–23.CrossRefGoogle Scholar
4. Yaglom, I. M. and Boltyanskiĭ, V. G.. Convex Figures (Holt, Rinehart and Winston, 1961).Google Scholar