Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T17:49:18.971Z Has data issue: false hasContentIssue false
  • English
  • Français

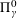ON THE $\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FE}}^{0}$-COMPLETENESS AND 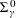$\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FE}}^{0}$-COMPLETENESS OF MULTIFRACTAL DECOMPOSITION SETS

Part of: Generalities Set theory Classical measure theory

Published online by Cambridge University Press:  06 February 2018

L. Olsen
L. Olsen*
Affiliation:
Department of Mathematics, University of St. Andrews, St. Andrews, Fife KY16 9SS, Scotland email [email protected]
Get access

Abstract

The purpose of this paper twofold. Firstly, we establish 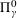$\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FE}}^{0}$-completeness and $\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FE}}^{0}$-completeness of several different classes of multifractal decomposition sets of arbitrary Borel measures (satisfying a mild non-degeneracy condition and two mild “smoothness” conditions). Secondly, we apply these results to study the 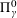$\unicode[STIX]{x1D6F1}_{\unicode[STIX]{x1D6FE}}^{0}$-completeness and 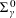$\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D6FE}}^{0}$-completeness of several multifractal decomposition sets of self-similar measures (satisfying a mild separation condition). For example, a corollary of our results shows if 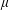$\unicode[STIX]{x1D707}$ is a self-similar measure satisfying the strong separation condition and 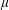$\unicode[STIX]{x1D707}$ is not equal to the normalized Hausdorff measure on its support, then the classical multifractal decomposition sets of 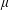$\unicode[STIX]{x1D707}$ defined by

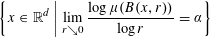$$\begin{eqnarray}\bigg\{x\in \mathbb{R}^{d}\,\bigg|\,\lim _{r{\searrow}0}\frac{\log \unicode[STIX]{x1D707}(B(x,r))}{\log r}=\unicode[STIX]{x1D6FC}\bigg\}\end{eqnarray}$$
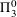are $\unicode[STIX]{x1D6F1}_{3}^{0}$-complete provided they are non-empty.

MSC classification

Primary: 03E15: Descriptive set theory
Secondary: 28A80: Fractals 54A05: Topological spaces and generalizations (closure spaces, etc.)
Type
Research Article
Information
Mathematika , Volume 64 , Issue 1 , 2018 , pp. 77 - 114
Copyright
Copyright © University College London 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barreira, L. and Schmeling, J., Sets of “non-typical” points have full topological entropy and full Hausdorff dimension. Israel J. Math. 116 2000, 29–70.Google Scholar
Falconer, K. J., Techniques in Fractal Geometry, John Wiley (Chichester, 1997).Google Scholar
Feng, D.-J. and Wu, J., The Hausdorff dimension of recurrent sets in symbolic spaces. Nonlinearity 14 2001, 81–85.Google Scholar
Hutchinson, J., Fractals and self-similarity. Indiana Univ. Math. J. 30 1981, 713–747.Google Scholar
Kechris, A., Classical Descriptive Set Theory (Graduate Texts in Mathematics 156 ), Springer (New York, 1994).Google Scholar
Ki, H. and Linton, T., Normal numbers and subsets of ℕ with given densities. Fund. Math. 144 1994, 163–179.Google Scholar
Louveau, A. and Saint Raymond, J., Borel classes and closed games: Wadge-type and Hurewicz-type results. Trans. Amer. Math. Soc. 304 1987, 431–467.Google Scholar
Mattila, P., On the structure of self-similar fractals. Ann. Acad. Sci. Fenn. Math. 7 1982, 189–195.Google Scholar
Olsen, L. and Winter, S., Normal and non-normal points of self-similar sets and divergence points of self-similar measures. J. Lond. Math. Soc. (2) 67 2003, 103–122.Google Scholar
Pesin, Y., Dimension Theory in Dynamical Systems. Contemporary Views and Applications, University of Chicago Press (Chicago, 1997).CrossRefGoogle Scholar