Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Greaves, George
1971.
Large prime factors of binary forms.
Journal of Number Theory,
Vol. 3,
Issue. 1,
p.
35.
Hooley, C.
1973.
On the largest prime factor of
p
+
a
.
Mathematika,
Vol. 20,
Issue. 2,
p.
135.
Murata, Leo
1980.
On certain averages of $\omega \left( n \right)$.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 56,
Issue. 10,
Pomerance, Carl
1980.
Popular values of Euler's function.
Mathematika,
Vol. 27,
Issue. 1,
p.
84.
Maurer, Ueli M.
1995.
Fast generation of prime numbers and secure public-key cryptographic parameters.
Journal of Cryptology,
Vol. 8,
Issue. 3,
p.
123.
Baker, R. C.
and
Harman, G.
1996.
Analytic Number Theory.
p.
39.
Granville, Andrew
2004.
It is easy to determine whether a given integer is prime.
Bulletin of the American Mathematical Society,
Vol. 42,
Issue. 1,
p.
3.
Borwein, Peter
Choi, Stephen
Rooney, Brendan
and
Weirathmueller, Andrea
2008.
The Riemann Hypothesis.
p.
161.
Bornemann, Folkmar
2008.
π und Co..
p.
55.
Baker, Roger
2009.
Numbers in a given set with (or without) a large prime factor.
The Ramanujan Journal,
Vol. 20,
Issue. 3,
p.
275.
Felix, Adam Tyler
and
Murty, M. Ram
2012.
ON A CONJECTURE OF ERDŐS.
Mathematika,
Vol. 58,
Issue. 2,
p.
275.
Meng, X.
2015.
On the number of strong primes.
Acta Mathematica Hungarica,
Vol. 145,
Issue. 2,
p.
505.
Chen, Feng Juan
and
Chen, Yong Gao
2017.
On the largest prime factor of shifted primes.
Acta Mathematica Sinica, English Series,
Vol. 33,
Issue. 3,
p.
377.
Feng, Bin
and
Wu, Jie
2018.
On the density of shifted primes with large prime factors.
Science China Mathematics,
Vol. 61,
Issue. 1,
p.
83.
WU, JIE
2019.
ON VALUES TAKEN BY THE LARGEST PRIME FACTOR OF SHIFTED PRIMES.
Journal of the Australian Mathematical Society,
Vol. 107,
Issue. 1,
p.
133.
Lü, Xiaodong
Wang, Zhiwei
and
Chen, Bin
2019.
On the smooth values of shifted almost-primes.
International Journal of Number Theory,
Vol. 15,
Issue. 01,
p.
1.
Wang, Zhiwei
2021.
Three conjectures on P+(n) and P+(n + 1) hold under the Elliott-Halberstam conjecture for friable integers.
Journal of Number Theory,
Vol. 223,
Issue. ,
p.
1.
Nath, Ayan
and
Jha, Abhishek
2022.
On the least common multiple of polynomial sequences at prime arguments.
International Journal of Number Theory,
Vol. 18,
Issue. 06,
p.
1227.
Borsos, B.
Kovács, A.
and
Tihanyi, N.
2023.
On reciprocal sums of infinitely many arithmetic progressions with increasing prime power moduli.
Acta Mathematica Hungarica,
Vol. 171,
Issue. 2,
p.
203.
Ding, Yuchen
2023.
On a conjecture on shifted primes with large prime factors.
Archiv der Mathematik,
Vol. 120,
Issue. 3,
p.
245.
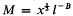 with l = log x, then for x > 1
with l = log x, then for x > 1