Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-26T17:26:54.933Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE MONOTONICITY OF THE MOMENTS OF VOLUMES OF RANDOM SIMPLICES

Part of: General convexity Geometric probability and stochastic geometry

Published online by Cambridge University Press:  01 June 2016

Benjamin Reichenwallner  and
Matthias Reitzner
Benjamin Reichenwallner
Affiliation:
Fachbereich Mathematik, Universität Salzburg, Hellbrunnerstraße 34, 5020 Salzburg, Austria email [email protected]
Matthias Reitzner
Affiliation:
Institut für Mathematik, Universität Osnabrück, Albrechtstr. 28a, D-49076 Osnabrück, Germany email [email protected]
Get access

Abstract

In a 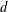$d$ -dimensional convex body 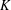$K$ random points 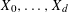$X_{0},\ldots ,X_{d}$ are chosen. Their convex hull is a random simplex. The expected volume of a random simplex is monotone under set inclusion if 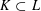$K\subset L$ implies that the expected volume of a random simplex in 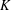$K$ is smaller than the expected volume of a random simplex in 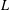$L$ . Continuing work of Rademacher [On the monotonicity of the expected volume of a random simplex. Mathematika58 (2012), 77–91], it is shown that moments of the volume of random simplices are, in general, not monotone under set inclusion.

MSC classification

Primary: 60D05: Geometric probability and stochastic geometry
Secondary: 52A22: Random convex sets and integral geometry
Type
Research Article
Information
Mathematika , Volume 62 , Issue 3 , 2016 , pp. 949 - 958
Copyright
Copyright © University College London 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alagar, V. S., On the distribution of a random triangle. J. Appl. Probab. 14 1977, 284–297.CrossRefGoogle Scholar
Borgwardt, K.-H., Some distribution-independent results about the asymptotic order of the average number of pivot steps of the simplex method. Math. Oper. Res. 7 1982, 441–462.Google Scholar
Hug, D., Random polytopes. In Stochastic Geometry, Spatial Statistics and Random Fields (Lecture Notes in Mathematics 2068 ) (ed. Spodarev, E.), Springer (Heidelberg, 2013), 205–238.Google Scholar
Meckes, M., Monotonicity of volumes of random simplices. In Recent Trends in Convex and Discrete Geometry (2006), abstract book, January 13–14, San Antonio, Texas.Google Scholar
Miles, R. E., Isotropic random simplices. Adv. Appl. Probab. 3 1971, 353–382.CrossRefGoogle Scholar
Rademacher, L., On the monotonicity of the expected volume of a random simplex. Mathematika 58 2012, 77–91.CrossRefGoogle Scholar
Reed, W. J., Random points in a simplex. Pacific J. Math. 54 1974, 183–198.Google Scholar
Reitzner, M., Random polytopes. In New Perspectives in Stochastic Geometry (eds Kendall, W. S. and Molchanov, I.), Oxford University Press (Oxford, 2010), 45–76.Google Scholar
Schneider, R. and Weil, W., Stochastic and integral geometry. In Probability and its Applications (New York), Springer (Berlin, 2008).Google Scholar
Solomon, H., Geometric probability. In Regional Conference Series in Applied Mathematics, Vol. 28, SIAM (Philadelphia, PA, 1978).Google Scholar