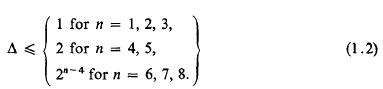Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-05T19:47:14.651Z Has data issue: false hasContentIssue false
  • English
  • Français

On the minimum points of a positive quadratic form

Published online by Cambridge University Press:  26 February 2010

G. L. Watson
G. L. Watson
Affiliation:
University College, London.
Get access

Extract

Let fn be a positive-definite n-ary quadratic form, with real coefficients. By the minimum of fn, denoted by min fn, is meant as usual the least value of fn(x1, …, xn) for integers xi not all 0. A minimum point of fn is a point x = (x1, …, xn), with integer coordinates, at which fn takes its minimum value. Let Δ (> 0) be the determinant of a set of n minimum points of fn; then in [1] it was proved that

where γn is the Hermite constant. Enough is known about γn to deduce from (1.1), as in [1], that

Type
Research Article
Information
Mathematika , Volume 18 , Issue 1 , June 1971 , pp. 60 - 70
Copyright
Copyright © University College London 1971

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Davenport, H. and Watson, G. L., “The minimal points of a positive definite quadratic form”, Mathematika, 1 (1954), 14–17.CrossRefGoogle Scholar
2.Korkine, A. and Zolotareff, G., “Sur les formes quadratiques positives”, Math. Ann., 11 (1877), 242–292.CrossRefGoogle Scholar
3.Blichfeldt, H. F., “The minimum values of positive quadratic forms in six, seven and eight variables”, Math. Z., 39 (1935), 1–15.CrossRefGoogle Scholar
4.Barnes, E. S., “The complete enumeration of extreme senary forms”, Philos. Trans. Roy. Soc, London, A, 249 (1957), 461–506.Google Scholar
5.Watson, G. L., “On the minimal points of perfect septenary quadratic forms”, Mathematika, 16 (1969), 170–177.CrossRefGoogle Scholar