Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Jiang, Yujiao
and
Lü, Guangshi
2019.
On automorphic analogues of the Möbius randomness principle.
Journal of Number Theory,
Vol. 197,
Issue. ,
p.
268.
HU, DANIEL
KANEKO, IKUYA
MARTIN, SPENCER
and
SCHILDKRAUT, CARL
2024.
On a Mertens-type conjecture for number fields.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 177,
Issue. 3,
p.
481.


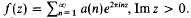 We assume further that
We assume further that