Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Tu Cuong, Nguyen
1990.
On the length of the powers of systems of parameters in local ring.
Nagoya Mathematical Journal,
Vol. 120,
Issue. ,
p.
77.
Cuong, Nguyen Tu
1992.
On the least degree of polynomials bounding above the differences between lengths and multiplicities of certain systems of parameters in local rings.
Nagoya Mathematical Journal,
Vol. 125,
Issue. ,
p.
105.
Cuong, Nguyen Tu
and
Khoi, Vu The
1996.
On the partial Euler-Poincare characteristics of certain systems of parameters in local rings.
Mathematische Zeitschrift,
Vol. 222,
Issue. 3,
p.
383.
Cuong, Nguyen Tu
and
Nhan, Le Thanh
2003.
Pseudo Cohen–Macaulay and pseudo generalized Cohen–Macaulay modules.
Journal of Algebra,
Vol. 267,
Issue. 1,
p.
156.
CUONG, NGUYEN TU
and
CUONG, DOAN TRUNG
2007.
dd-SEQUENCES AND PARTIAL EULER–POINCARÉ CHARACTERISTICS OF KOSZUL COMPLEX.
Journal of Algebra and Its Applications,
Vol. 06,
Issue. 02,
p.
207.
Nam, Pham Hong
2024.
ON THE PARTIAL EULER–POINCARÉ CHARACTERISTICS OF KOSZUL COMPLEXES OF IDEALIZATION.
Journal of Commutative Algebra,
Vol. 16,
Issue. 1,


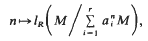
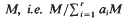 has finite length.
has finite length.