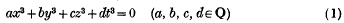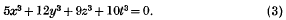Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
1969.
Vol. 30,
Issue. ,
p.
82.
Zimmer, Horst G.
1971.
Some computational aspects of, and the use of computers in, algebraic number theory.
Computing,
Vol. 8,
Issue. 3-4,
p.
363.
Parshin, A. N.
1973.
Arithmetic on algebraic varieties.
Journal of Soviet Mathematics,
Vol. 1,
Issue. 5,
p.
594.
Bremner, Andrew
1978.
Some cubic surfaces with no rational points.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 84,
Issue. 2,
p.
219.
Grosswald, Emil
1984.
Topics from the Theory of Numbers.
p.
255.
1986.
Cubic Forms - Algebra, Geometry, Arithmetic.
Vol. 4,
Issue. ,
p.
318.
Colliot-Thélène, Jean-Louis
and
Sansuc, Jean-Jacques
1987.
La descente sur les variétés rationnelles, II.
Duke Mathematical Journal,
Vol. 54,
Issue. 2,
Colliot-Thélène, Jean-Louis
Kanevsky, Dimitri
and
Sansuc, Jean-Jacques
1987.
Diophantine Approximation and Transcendence Theory.
Vol. 1290,
Issue. ,
p.
1.
Heath-Brown, D. R.
1992.
The density of zeros of forms for which weak approximation fails.
Mathematics of Computation,
Vol. 59,
Issue. 200,
p.
613.
Vaughan, R. C.
and
Wooley, T. D.
1995.
On a certain nonary cubic form and related equations.
Duke Mathematical Journal,
Vol. 80,
Issue. 3,
Colliot-Thélène, Jean-Louis
and
Poonen, Bjorn
1999.
Algebraic families of nonzero elements of Shafarevich-Tate groups.
Journal of the American Mathematical Society,
Vol. 13,
Issue. 1,
p.
83.
Wooley, Trevor D.
1999.
Topics in Number Theory.
p.
49.
Harari, David
2004.
Arithmetic of Higher-Dimensional Algebraic Varieties.
Vol. 226,
Issue. ,
p.
43.
Swinnerton-Dyer, Peter
2005.
The justification of mathematical statements.
Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 363,
Issue. 1835,
p.
2437.
Stoll, Michael
2007.
Finite descent obstructions and rational points on curves.
Algebra & Number Theory,
Vol. 1,
Issue. 4,
p.
349.
Heath-Brown, D.R.
2007.
Cubic forms in 14 variables.
Inventiones mathematicae,
Vol. 170,
Issue. 1,
p.
199.
Várilly-Alvarado, Anthony
2008.
Weak approximation on del Pezzo surfaces of degree 1.
Advances in Mathematics,
Vol. 219,
Issue. 6,
p.
2123.
Kresch, Andrew
and
Tschinkel, Yuri
2008.
Effectivity of Brauer–Manin obstructions.
Advances in Mathematics,
Vol. 218,
Issue. 1,
p.
1.
Narkiewicz, Władysław
2012.
Rational Number Theory in the 20th Century.
p.
131.
Elsenhans, Andreas-Stephan
and
Jahnel, Jörg
2013.
Experiments with the transcendental Brauer-Manin obstruction.
The Open Book Series,
Vol. 1,
Issue. 1,
p.
369.