Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T18:51:21.814Z Has data issue: false hasContentIssue false
  • English
  • Français

On the distribution of gaps between squarefree numbers

Part of: Multiplicative number theory

Published online by Cambridge University Press:  26 February 2010

Michael Filaseta
Michael Filaseta
Affiliation:
Mathematics Department, University of South Carolina, Columbia, SC 29208, U.S.A.
Get access

Extract

Let s1, s2, … denote the squarefree numbers in ascending order. In [1], Erdős showed that, if 0 ≤ γ ≤ 2, then

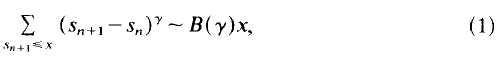
where B(γ) is a function only of γ. In 1973 Hooley [4] improved the range of validity of this result to 0 ≤ γ ≤ 3, and then later gained a further slight improvement by a method he outlined at the International Number Theory Symposium at Stillwater, Oklahoma in 1984. We have, however, independently obtained the better improvement that (1) holds for

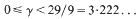
in contrast to the range

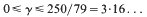
derived by Hooley. The main purpose of this paper is to substantiate our new result. Professor Hooley has informed me that there are similarities between our methods as well as significant differences.

MSC classification

Secondary: 11N25: Distribution of integers with specified multiplicative constraints
Type
Research Article
Information
Mathematika , Volume 40 , Issue 1 , June 1993 , pp. 88 - 101
Copyright
Copyright © University College London 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Erdős, P.. Some problems and results in elementary number theory. Publ. Math. Debrecen, 2 (1951), 103–109.Google Scholar
2.Filaseta, M. and Trifonov, O.. On gaps between squarefree numbers. Analytic Number Theory, Proceedings of a Conference in Honor of Paul T. Bateman (Progress in Mathematics Series, Vol. 85), edited by Berndt, , Halberstam, Diamond, and Hildebrand, (Birkhäuser, Boston, 1990), 235–253.CrossRefGoogle Scholar
3.Filaseta, M. and Trifonov, O.. On gaps between squarefree numbers II. j. London Math. Soc. (2), 45 (1992), 215–221.CrossRefGoogle Scholar
4.Hooley, C.. On the distribution of square-free numbers. Can. J. Math., 25 (1973), 1216–1223.Google Scholar
5.Mirsky, L.. Arithmetical pattern problems related to divisibility by r-th powers. Proc. London Math. Soc, 50 (1949), 497–508.Google Scholar
6.Trifonov, O.. On the squarefree problem. C. R. Acad. Bulgare Sci., 41 (1988), 37–40.Google Scholar
7.Trifonov, O.. On the squarefree problem II. Mathematica Balcanika, 3 (1989), 284–295.Google Scholar