Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-23T12:17:10.540Z Has data issue: false hasContentIssue false
  • English
  • Français

On the classgroup of integral grouprings of finite abelian groups

Published online by Cambridge University Press:  26 February 2010

A. Fröhlich
A. Fröhlich
Affiliation:
University of London King's College, Strand, London, W.C.2.
Get access

Extract

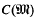Let Z(Γ) be the integral groupring of a finite Abelian group Γ. There is some interest in the study of its class group (Picard group) C(Z(Γ)) (cf. e.g. [1] and [5]). One knows that this group is mapped surjectively onto the class group of the maximal order 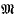in the rational groupring Q(Γ). Now 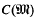is known in the sense that it is the product of the classgroups of the algebraic integer rings, whose quotient fields appear in the decomposition of Q(Γ). One is thus also interested in the kernel D(Z(Γ)) of the map 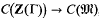, and it is this which concerns us here. I shall show that it can become very big.

Type
Research Article
Information
Mathematika , Volume 16 , Issue 2 , December 1969 , pp. 143 - 152
Copyright
Copyright © University College London 1969

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Bass, Hyman, Algebraic K-Theory (Benjamin, New York, 1968).Google Scholar
2.Higman, G., “The units of group rings”, Proc. London Math. Soc. (2), 46 (1940), 231–248.CrossRefGoogle Scholar
3.Rim, Dock Sang, “Modules over finite groups“, Ann. of Math. (2), 69 (1959), 700–712.CrossRefGoogle Scholar
4.Serre, J-P., “Modules projectifs et espaces fibrés a fibre vectorielle“, Sént. Dubreil-Pisot (1957/58).Google Scholar
5.Wall, C. T. C., “An obstruction to finiteness of C. W. complexes, Bull. Amer. Math. Soc., 70 (1964), 269–270.CrossRefGoogle Scholar