No CrossRef data available.
Published online by Cambridge University Press: 26 February 2010
We consider the second order linear differential equation
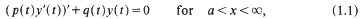
where p and q are real-valued members of 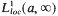 with p(t)>0 for t ∈ [α, ∞). In particular we consider the following three questions dealing with the asymptotic behavior of solutions of (1.1).
with p(t)>0 for t ∈ [α, ∞). In particular we consider the following three questions dealing with the asymptotic behavior of solutions of (1.1).