No CrossRef data available.
Published online by Cambridge University Press: 26 February 2010
Recall that a Poincaré Duality group G is said to be smoothly realisable when there exists a smooth closed manifold XG of homotopy type K(G, 1). In this note we prove
Theorem 1. Let
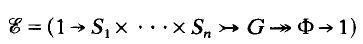
be an exact sequence of groups in which each Si is a Surface group, with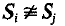 for i ≠ j, Ф is finite and G is torsion free. Then the Poincaré Duality group G is smoothly realisable.
for i ≠ j, Ф is finite and G is torsion free. Then the Poincaré Duality group G is smoothly realisable.