Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-26T01:09:07.130Z Has data issue: false hasContentIssue false
  • English
  • Français

ON SIGN CHANGES FOR ALMOST PRIME COEFFICIENTS OF HALF-INTEGRAL WEIGHT MODULAR FORMS

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  06 May 2016

Srilakshmi Krishnamoorthy  and
M. Ram Murty
Srilakshmi Krishnamoorthy
Affiliation:
Department of Mathematics, Indian Institute of Technology Madras, Chennai 600036, India email [email protected]
M. Ram Murty
Affiliation:
Department of Mathematics, Queen’s University, Kingston, Ontario, K7L 3N6, Canada email [email protected]
Get access

Abstract

For a half-integral weight modular form 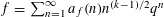$f=\sum _{n=1}^{\infty }a_{f}(n)n^{(k-1)/2}q^{n}$ of weight 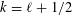$k=\ell +1/2$ on 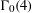$\unicode[STIX]{x1D6E4}_{0}(4)$ such that 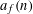$a_{f}(n)$ ( 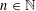$n\in \mathbb{N}$ ) are real, we prove for a fixed suitable natural number $r$ that 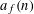$a_{f}(n)$ changes sign infinitely often as $n$ varies over numbers having at most $r$ prime factors, assuming the analog of the Ramanujan conjecture for Fourier coefficients of half-integral weight forms.

MSC classification

Primary: 11F37: Forms of half-integer weight; nonholomorphic modular forms 11F11: Holomorphic modular forms of integral weight
Secondary: 11F30: Fourier coefficients of automorphic forms
Type
Research Article
Information
Mathematika , Volume 62 , Issue 3 , 2016 , pp. 801 - 810
Copyright
Copyright © University College London 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Blomer, V. and Harcos, G., Hybrid bounds for twisted L-functions. J. Reine Angew. Math. 621 2008, 53–79.Google Scholar
Cojocaru, A. C. and Murty, M. R., An Introduction to Sieve Methods and Their Applications (London Mathematical Society Student Texts 66 ), Cambridge University Press (Cambridge, 2006).Google Scholar
Duke, W. and Iwaniec, H., Bilinear forms in the Fourier coefficients of half-integral weight cusp forms and sums over primes. Math. Ann. 286(4) 1990, 783–802.CrossRefGoogle Scholar
Halberstam, H. and Richert, H.-E., Sieve Methods, Academic Press (London, 1974).Google Scholar
Hoffstein, J. and Luo, W., Nonvanishing of L-series and the combinatorial sieve. Math. Res. Lett. 4 1997, 435–444, with an appendix by David E. Rohrlich.CrossRefGoogle Scholar
Hulse, T. A., Kiral, E. M., Kuan, C. I. and Lim, L., The sign of Fourier coefficients of half-integral weight cusp forms. Int. J. Number Theory 8 2012, 749–762.CrossRefGoogle Scholar
Iwaniec, H., Fourier coefficients of modular forms of half-integral weight. Invent. Math. 87(2) 1987, 385–401.CrossRefGoogle Scholar
Kohnen, W., On Hecke eigenforms of half-integral weight. Math. Ann. 293(3) 1992, 427–431.CrossRefGoogle Scholar
Kohnen, W., A short note on Fourier coefficients of half-integral weight modular forms. Int. J. Number Theory 6 2010, 1255–1259.CrossRefGoogle Scholar
Kohnen, W. and Zagier, D., Values of L-series of modular forms at the center of the critical strip. Invent. Math. 64 1981, 175–198.CrossRefGoogle Scholar
Meher, J. and Murty, M. R., Sign changes of Fourier coefficients of half-integral weight cusp forms. Int. J. Number Theory 10(4) 2014, 905–914.CrossRefGoogle Scholar
Moreno, C. J., The Hoheisel phenomenon for generalized Dirichlet series. Proc. Amer. Math. Soc. 40 1973, 47–51.CrossRefGoogle Scholar
Murty, M. R., Oscillations of Fourier coefficients of modular forms. Math. Ann. 262 1983, 431–446.CrossRefGoogle Scholar
Murty, M. R. and Murty, V. K., Mean values of derivatives of modular L-series. Ann. of Math. (2) 133 1991, 447–475.CrossRefGoogle Scholar
Murty, M. R. and Murty, V. K., Non-vanishing of L-functions and applications (Progress in Mathematics 157 ), Birkhäuser (Basel, 1997).Google Scholar
Murty, M. R. and Sankaranarayanan, A., Averages of exponential twists of the Liouville function. Forum Math. 14 2002, 273–291.CrossRefGoogle Scholar
Shimura, G., On modular forms of half integral weight. Ann. of Math. (2) 97 1973, 440–481.CrossRefGoogle Scholar
Vaughan, R. C., Mean value theorems in prime number theory. J. Lond. Math. Soc. (2) 10 1975, 153–162.CrossRefGoogle Scholar
Waldspurger, J.-L., Sur les coefficients de Fourier des formes modulaires de poids demi-entier. J. Math. Pures Appl. (9) 60(4) 1981, 375–484.Google Scholar