Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T16:55:00.997Z Has data issue: false hasContentIssue false
  • English
  • Français

ON SELMER GROUPS AND TATE–SHAFAREVICH GROUPS FOR ELLIPTIC CURVES y2=x3−n3

Part of: Exponential sums and character sums Multiplicative number theory Curves Arithmetic algebraic geometry

Published online by Cambridge University Press:  12 April 2012

Keqin Feng  and
Maosheng Xiong
Keqin Feng
Affiliation:
Department of Mathematical Science, Tshinghua University, Beijing 100084, P.R. China (email: [email protected])
Maosheng Xiong
Affiliation:
Department of Mathematics, Hong Kong University of Science and Technology, Clear Water Bay, Kowloon, P.R. China (email: [email protected])
Get access

Abstract

We study the distribution of the size of Selmer groups and Tate–Shafarevich groups arising from a 2-isogeny and its dual 2-isogeny for elliptic curves En:y2=x3−n3. We show that the 2-ranks of these groups all follow the same distribution. The result also implies that the mean value of the 2-rank of the corresponding Tate–Shafarevich groups for square-free positive integers n≤X is 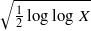as X→∞. This is quite different from quadratic twists of elliptic curves with full 2-torsion points over ℚ [M. Xiong and A. Zaharescu, Distribution of Selmer groups of quadratic twists of a family of elliptic curves. Adv. Math. 219 (2008), 523–553], where one Tate–Shafarevich group is almost always trivial while the other is much larger.

MSC classification

Secondary: 11G05: Elliptic curves over global fields 14H52: Elliptic curves 11L40: Estimates on character sums 11N45: Asymptotic results on counting functions for algebraic and topological structures
Type
Research Article
Information
Mathematika , Volume 58 , Issue 2 , July 2012 , pp. 236 - 274
Copyright
Copyright © University College London 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Aoki, N., On the 2-Selmer groups of elliptic curves arising from the congruent number problems. Comment. Math. Univ. St. Pauli. 48 (1999), 77–101.Google Scholar
[2]Aoki, N., On the Tate–Shafarevich group of semistable elliptic curves with a rational 3-torsion. Acta Arith. 112(3) (2004), 209–227.Google Scholar
[3]Atake, D., On elliptic curves with large Tate–Shafarevich groups. J. Number Theory 87 (2001), 282–300.CrossRefGoogle Scholar
[4]Bölling, R., Die Ordnung der Schafarewitsch–Tate–Gruppe kann beliebig großwerden. Math. Nachr. 67 (1975), 157–179.CrossRefGoogle Scholar
[5]Cassels, J. W. S., Arithmetic on curves of genus 1. VI. The Tate–Shafarevich group can be arbitrarily large. J. Reine Angew. Math. 214 (1963), 65–70.Google Scholar
[6]Chang, S., Note on the rank of quadratic twists of Mordell equations. J. Number Theory 118(1) (2006), 53–61.CrossRefGoogle Scholar
[7]Delaunay, C., Heuristics on Tate–Shafarevich groups of elliptic curves defined over ℚ. Experiment. Math. 10(2) (2001), 191–196.CrossRefGoogle Scholar
[8]Delaunay, C., Moments of the orders of Tate–Shafarevich groups. Int. J. Number Theory 1(2) (2005), 243–264.CrossRefGoogle Scholar
[9]Faulkner, B. and James, K., A graphical approach to computing Selmer groups of congruent number curves. Ramanujan J. 14(1) (2007), 107–129.CrossRefGoogle Scholar
[10]Feng, K., On the rank and the BSD conjecture of elliptic curves E D:y 2=x 3−D 3. In Algebraic Geometry and Algebraic Number Theory (Tianjin, 1989–1990) (Nankai series in pure, applied mathematics and theoretical physics 3), World Scientific (River Edge, NJ, 1992), 24–34.Google Scholar
[11]Feng, K., Non-congruent numbers, odd graph and BSD conjecture on y 2=x 3−n 2x. Acta. Arith. 75 (1996), 71–83.CrossRefGoogle Scholar
[12]Feng, K. and Xiong, M., On elliptic curves y 2=x 3−n 2x with rank zero. J. Number Theory 109(1) (2004), 1–26.CrossRefGoogle Scholar
[13]Feng, K. and Xue, Y., New series of odd non-congruent numbers. Sci. China Ser. A 49(11) (2006), 1642–1654.CrossRefGoogle Scholar
[14]Goldfeld, D. and Lieman, D., Effective bounds on the size of the Tate–Shafarevich group. Math. Res. Lett. 3(3) (1996), 309–318.CrossRefGoogle Scholar
[15]Goldfeld, D. and Szpiro, L., Bounds for the order of the Tate–Shafarevich group. Compositio Math. 97(1–2) (1995), 71–87.Google Scholar
[16]Granville, A. and Soundararajan, K., Sieving and the Erdős–Kac theorem. In Equidistribution in Number Theory, an introduction (NATO Science Series II Mathematics, Physics and Chemistry 237), Springer (Dordrecht, 2007), 15–27.Google Scholar
[17]Harris, J. M., Hirst, J. L. and Mossignhoff, M. J., Combinatorics and Graph Theory, Springer (Berlin, 2000).CrossRefGoogle Scholar
[18]Heath-Brown, D. R., The size of Selmer groups for the congruent number problem, I. Invent. Math. 111 (1993), 171–195.CrossRefGoogle Scholar
[19]Heath-Brown, D. R., The size of Selmer groups for the congruent number problem, II. Invent. Math. 118 (1994), 331–370.CrossRefGoogle Scholar
[20]Kloosterman, R., The p-part of the Tate–Shafarevich groups of elliptic curves can be arbitrarily large. J. Théor. Nombres Bordeaux 17(3) (2005), 787–800.CrossRefGoogle Scholar
[21]Kramer, K., A family of semistable elliptic curves with large Tate–Shafarevich groups. Proc. Amer. Math. Soc. 89 (1983), 379–386.CrossRefGoogle Scholar
[22]Lemmermeyer, F., On Tate–Shafarevich groups of some elliptic curves. In Algebraic Number Theory and Diophantine Analysis (Graz, 1998), de Gruyter (Berlin, 2000), 277–291.Google Scholar
[23]Lemmermeyer, F. and Mollin, R., On Tate–Shafarevich groups of y2=x(x2−k2). Acta Math. Univ. Comenian. (N.S.) 72(1) (2003), 73–80.Google Scholar
[24]Nakagawa, J. and Horie, K., Elliptic curves with no rational points. Proc. Amer. Math. Soc. 104 (1988), 20–24.CrossRefGoogle Scholar
[25]Silverman, J. H., The Arithmetic of Elliptic Curves (Graduate Texts in Mathematics 106), Springer (Berlin, 1986).CrossRefGoogle Scholar
[26]Stoll, M., On the arithmetic of the curves y 2=x l+A and their Jacobians. J. Reine Angew. Math. 501 (1998), 171–189.CrossRefGoogle Scholar
[27]Stoll, M., On the arithmetic of the curves y 2=x l+A. II. J. Number Theory 93(2) (2002), 183–206.CrossRefGoogle Scholar
[28]Swinnerton-Dyer, P., The effect of twisting on the 2-Selmer group. Math. Proc. Cambridge Philos. Soc. 145(3) (2008), 513–526.CrossRefGoogle Scholar
[29]Xiong, M. and Zaharescu, A., Distribution of Selmer groups of quadratic twists of a family of elliptic curves. Adv. Math. 219 (2008), 523–553.CrossRefGoogle Scholar
[30]Yu, G., Rank 0 quadratic twists of a family of elliptic curves. Compositio Math. 135(3) (2003), 331–356.CrossRefGoogle Scholar
[31]Yu, G., Average size of 2-Selmer groups of elliptic curves. II. Acta. Arith. 117(1) (2005), 1–33.CrossRefGoogle Scholar
[32]Yu, G., On the quadratic twists of a family of elliptic curves. Mathematika 52(1–2) (2006), 139–154.CrossRefGoogle Scholar