Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T19:29:41.714Z Has data issue: false hasContentIssue false
  • English
  • Français

On plane coverings with convex domains

Published online by Cambridge University Press:  26 February 2010

R. P. Bambah  and
A. C. Woods
R. P. Bambah
Affiliation:
Panjab University, Chandigarh, India.
A. C. Woods
Affiliation:
The Ohio State University, Columbus, Ohio
Get access

Extract

The following theorem has been proved by Bambah, Rogers and Zassenhaus [1],

Theorem A. Let K be a closed convex domain with a centre. Let

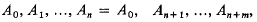
be points such that:

(i) the polygon A0 A1 … An is a Jordan polygon bounding a closed domain π of area a(π);

(ii) for each r, 0 ≤ r ≤ n, there is a point common to K + An-1 and K + Ar;

(iii) the points An+1, …. An+m are in the interior of π;

(iv) for each point X of π, there exists an Ar, 1 ≤ r ≤ n + m, such that X ∈ K + Ar and the line segment XAr is in π. Then

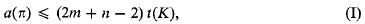
where t(K) is the area of the largest triangle contained in K.

Type
Research Article
Information
Mathematika , Volume 18 , Issue 1 , June 1971 , pp. 91 - 97
Copyright
Copyright © University College London 1971

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Bambah, R. P., Rogers, C. A. and Zassenhaus, H., “On coverings with convex domains”, Acta Arithmetica, 9 (1964), 191–207.CrossRefGoogle Scholar
2.Fejes Tóth, L., “Some packing and covering theorems”, Acta. Sci. Math. Szeged, 12 (1950), 62–67.Google Scholar
3.Bambah, R. P. and Rogers, C. A., “Covering the plane with convex sets”, J. London. Math. Soc, 27 (1952), 304–314.CrossRefGoogle Scholar
4.Zassenhaus, H., “Modern developments in the geometry of numbers”, Bull. Amer. Math. Soc, 67 (1961), 427–439.CrossRefGoogle Scholar