Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T19:07:32.191Z Has data issue: false hasContentIssue false
  • English
  • Français

On minimal pairs and residually transcendental extensions of valuations

Part of: Topological fields

Published online by Cambridge University Press:  26 February 2010

Sudesh K. Khanduja ,
N. Popescu  and
K. W. Roggenkamp
Sudesh K. Khanduja
Affiliation:
Departmcnt of Mathematics, Punjab University. Chandigarh-160014. India. E-mail:[email protected]
N. Popescu
Affiliation:
Institute of Mathematics of the Romanian, Academy, P.O. Box 1-764, Bucharest 70700, Romania. E-mail:[email protected]
K. W. Roggenkamp
Affiliation:
Mathcmatisches Institut B, Universitat Stuttgart, Pfaffenwaldring 57, D-70550 Stuttgart, Germany. E-mail:[email protected]
Get access

Abstract

In this paper, further insight is obtained into the earlier approach of studying residually transcendental extensions of a valuation v of a field K to a simple transcendental extension K(x) of K by means of minimal pairs, thereby introducing new invariants corresponding to any element of an algebraic closure 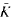of K. It is also shown that these invariants are of independent interest as well. A characterization of those elements a belonging to 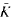is given such that there exists a minimal pair (a, δ) for some δ in the divisible closure of the value group of v.

MSC classification

Secondary: 12J10: Valued fields
Type
Research Article
Information
Mathematika , Volume 49 , Issue 1-2 , June 2002 , pp. 93 - 106
Copyright
Copyright © University College London 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Aghigh, K. and Khanduja, S. K.. On the main invariant of elemcnts algebraic over a Henselian valued field. Proc. Edinburgh Math. Soc., 45 (2002), 219–227.CrossRefGoogle Scholar
2.Alexandra, V.. Popescu, N. and Zaharcscu, A.. A theorem of characterization of residual transcendenlal extensions of a valuation. J. Math. Kyoto Univ., 28 (1988), 579–592.Google Scholar
3.Alexandra, V.. Popescu, N. and Zahareseu, A.. Minimal pairs of a residual transcendental extension of a valuation. J. Math. Kyoto Univ., 30 (1990), 207–225.Google Scholar
4.Alexandra, V.. Popescu, N. and Zahareseu, A.. All valuations on K(X). J. Math. Kyoto Univ., 30 (1990). 281–296.Google Scholar
5.Ax, J.. Zeros of polynomials over local fields The Galois action. J. Algebra, 15 (1970). 417–428.CrossRefGoogle Scholar
6.Bourbaki, N.. Théorie des Ensembles (Hermann, Paris. 1956).Google Scholar
7.Endler, O.. Wiluation Theory (Springer-Verlag).Google Scholar
8.Khanduja, S. K.. A note on a resulfof J. Ax. J. Algebra, 140 (1991), 360–361.CrossRefGoogle Scholar
9.Khanduja, S. K.. On valuations of K(x). Proc. Edinburgh Math. Soc., 35 (1992), 419–426.CrossRefGoogle Scholar
10.Khanduja, S. K. and Saha, Jayanti. Generalized fundamental principle. Mathematika. 46 (1999), 83–92.CrossRefGoogle Scholar
11.Kuhlmann, F.-V.. Henselian valued fields and lame fields (manuscript, 1990).Google Scholar
12.MacLane, S.. A construction for absolute values in polynomial rings. Trans. Anicr. Math. Soc., 40 (1936). 363–395.CrossRefGoogle Scholar
13.Nagata, M.. A theorem on valuation rings and its applications. Nagoya Math. J., 29 (1967). 85–91.CrossRefGoogle Scholar
14.Ohm, J.. Simple transcendental extensions of valued fields. J. Math. Kyoto Univ., 22 (1982), 201–221.Google Scholar
15.Ohm, J.. The ruled residue theorem for simple transcendental extensions of valued fields. Proc. Amer. Math. Soc., 89 (1983), 16–18.CrossRefGoogle Scholar
16.Ohm, J.. Simple transcendenlal extensions of valued fields, II: a fundamental inequality. J. Math. Kyoto Univ., 25 (1985), 583–596.Google Scholar
17.Popescu, N. and Zahareseu, A.. On the structure of irreducible polynomials over local fields. J. Number Th., 52(1) (1995). 98–118.CrossRefGoogle Scholar
18.Ostrowski, A.Untersuehungen zur arithmetischen Theoric der Körper. Math. Zeit., 39 (1934), 269–404.CrossRefGoogle Scholar