Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-22T16:17:35.390Z Has data issue: false hasContentIssue false
  • English
  • Français

ON LINEAR COMBINATIONS OF UNITS WITH BOUNDED COEFFICIENTS

Part of: Algebraic number theory: global fields Elementary number theory

Published online by Cambridge University Press:  31 May 2011

Jörg Thuswaldner  and
Volker Ziegler
Jörg Thuswaldner
Affiliation:
Chair of Mathematics and Statistics, University of Leoben, Franz-Josef-Strasse 18, A-8700 Leoben, Austria (email: [email protected])
Volker Ziegler
Affiliation:
Institute for Analysis and Computational Number Theory, Graz University of Technology, Steyrergasse 30/IV, A-8010 Graz, Austria (email: [email protected])
Get access

Abstract

Starting with a paper of Jacobson from the 1960s, many authors became interested in characterizing all algebraic number fields in which each integer is the sum of pairwise distinct units. Although there exist many partial results for number fields of low degree, a full characterization of these number fields is still not available. Narkiewicz and Jarden posed an analogous question for sums of units that are not necessarily distinct. In this paper we propose a generalization of these problems. In particular, for a given rational integer n we consider the following problem. Characterize all number fields for which every integer is a linear combination 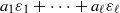of finitely many units εi in a way that the coefficients ai∈ℕ are bounded by n. The paper gives several partial results on this problem. In our proofs we exploit the fact that these representations are related to symmetric beta expansions with respect to Pisot bases.

MSC classification

Secondary: 11R16: Cubic and quartic extensions 11R11: Quadratic extensions 11A63: Radix representation; digital problems
Type
Research Article
Information
Mathematika , Volume 57 , Issue 2 , July 2011 , pp. 247 - 262
Copyright
Copyright © University College London 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Akiyama, S. and Scheicher, K., Symmetric shift radix systems and finite expansions. Math. Pannon. 18 (2007), 101–124.Google Scholar
[2]Artin, E., Theory of Algebraic Numbers (Notes by Gerhard Würges from Lectures held at the Mathematisches Institut, Göttingen, Germany, in the Winter Semester 1956/7), George Striker, Schildweg 12 (Göttingen, 1959).Google Scholar
[3]Ashrafi, N. and Vámos, P., On the unit sum number of some rings. Q. J. Math. 56(1) (2005), 1–12.CrossRefGoogle Scholar
[4]Barat, G., Berthé, V., Liardet, P. and Thuswaldner, J., Dynamical directions in numeration. Ann. Inst. Fourier (Grenoble) 56 (2006), 1987–2092.CrossRefGoogle Scholar
[5]Belcher, P., Integers expressible as sums of distinct units. Bull. Lond. Math. Soc. 6 (1974), 66–68.CrossRefGoogle Scholar
[6]Belcher, P., A test for integers being sums of distinct units applied to cubic fields. J. Lond. Math. Soc. II. Ser. 12 (1976), 141–148.CrossRefGoogle Scholar
[7]Bérczes, A., Pethő, A. and Ziegler, V., Parameterized norm form equations with arithmetic progressions. J. Symbolic Comput. 41(7) (2006), 790–810.CrossRefGoogle Scholar
[8]Bosma, W., Cannon, J. and Playoust, C., The Magma algebra system. I. The user language. J. Symbolic Comput. 24(3–4) (1997), 235–265.CrossRefGoogle Scholar
[9]Filipin, A., Tichy, R. and Ziegler, V., The additive unit structure of pure quartic complex fields. Funct. Approx. Comment. Math. 39 (2008), 113–131.CrossRefGoogle Scholar
[10]Frougny, C. and Solomyak, B., Finite beta-expansions. Ergod. Th. & Dynam. Sys. 12 (1992), 713–723.CrossRefGoogle Scholar
[11]Jacobson, B., Sums of distinct divisors and sums of distinct units. Proc. Amer. Math. Soc. 15 (1964), 179–183.CrossRefGoogle Scholar
[12]Jarden, M. and Narkiewicz, W., On sums of units. Monatsh. Math. 150(4) (2007), 327–336.CrossRefGoogle Scholar
[13]Lang, S., Algebraic Number Theory (Graduate Texts in Mathematics 110), Springer (New York, 1994).CrossRefGoogle Scholar
[14]Lemmermeyer, F. and Pethő, A., Simplest cubic fields. Manuscripta Math. 88 (1995), 53–58.CrossRefGoogle Scholar
[15]Narkiewicz, W., Elementary and Analytic Theory of Algebraic Numbers, 2nd edn., Springer (Berlin, 1990).Google Scholar
[16]Neukirch, J., Algebraic Number Theory (Grundlehren der Mathematischen Wissenschaften 322), Springer (Berlin, 1999).CrossRefGoogle Scholar
[17] The PARI Group, Bordeaux. PARI/GP, version 2.1.5, 2004. Available from http://pari.math.u-bordeaux.fr/.Google Scholar
[18]Śliwa, J., Sums of distinct units. Bull. Acad. Pol. Sci. 22 (1974), 11–13.Google Scholar
[19]Thomas, E., Fundamental units for orders in certain cubic number fields. J. Reine Angew. Math. 310 (1979), 33–55.Google Scholar
[20]Tichy, R. and Ziegler, V., Units generating the ring of integers of complex cubic fields. Colloq. Math. 109(1) (2007), 71–83.CrossRefGoogle Scholar
[21]Ziegler, V., The additive unit structure of complex biquadratic fields. Glas. Mat. Ser. III 43(2) (2008), 293–307.CrossRefGoogle Scholar