Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T19:27:45.867Z Has data issue: false hasContentIssue false
  • English
  • Français

On irregularities of integer sequences

Published online by Cambridge University Press:  26 February 2010

S. L. G. Choi
S. L. G. Choi
Affiliation:
Department of Mathematics, University of British ColumbiaVancouver 8, B.C. Canada
Get access

Abstract

Let f(m;n) denote the largest integer so that, given any m integers a1 < … < am in [1, 2n], one can always choose f integers b1 < … < bf from [1, n], so that bi + bj = a1 (1 ≤ i ≤ j ≤ f; l ≤ l ≤ m) will never hold. Trivially f(m; n) ≥ n/ (m + 1). In this paper we shall attempt to improve upon this trivial bound by exploiting the possible irregularities of distribution of the sequence among certain congruence classes. One of our main results is

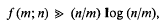
provided m ≥ log n. Related questions and results are also discussed.

Type
Research Article
Information
Mathematika , Volume 21 , Issue 1 , June 1974 , pp. 101 - 106
Copyright
Copyright © University College London 1974

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Choi, S. L. G., Erdős, P., Szemerédi., E. “Some additive and multiplicative problems in number theory” (to appear).Google Scholar
2.Choi, S. L. G.. “On a combinatorial problem in number theory”, Proc. London Math. Soc, (3), 23 (1971), 629–642.CrossRefGoogle Scholar
3.Cassels, J. W. S.. An introduction to diophantine approximation (Cambridge University Press).Google Scholar
4.Erdős, P.. “Some remarks on the theory of graphs”, Bulletin Amer. Math. Soc, 53 (1947), 292–294.CrossRefGoogle Scholar