Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-23T04:53:25.190Z Has data issue: false hasContentIssue false
  • English
  • Français

On irredundant components of the kernel of an ideal

Published online by Cambridge University Press:  26 February 2010

J. L. Mott
J. L. Mott
Affiliation:
University of Kansas, Lawrence, Kansas, U.S.A.
Get access

Extract

Throughout this paper a ring will mean a commutative ring with identity element. If A is an ideal of the ring R and P is a minimal prime ideal of A, then the intersection Q of all P-primary ideals which contain A is called the isolated primary component of A belonging to P. The ideal Q can also be described as the set of all elements x∈R such that xr∈A for some r∈R\P. If {Pα} is the collection of all minimal prime ideals of A and Qα is the isolated primary component of A belonging to Pα, then 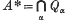is called the kernel of A.

Type
Research Article
Information
Mathematika , Volume 12 , Issue 1 , June 1965 , pp. 65 - 72
Copyright
Copyright © University College London 1965

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. JrGilmer, Robert W. and Mott, Leonard Joe, “Multiplication rings as rings in which ideals with prime radical are primary”, Trans. American Math. Soc., 114 (1965), 40–52.CrossRefGoogle Scholar
2. Krull, W., Idealtheorie (New York: Chelsea Publishing Co., 1948).CrossRefGoogle Scholar
3. Krull, W., “Idealtheorie in Ringen ohne Endlichkeitsbedingung”, Math. Ann., 29 (1928), 729–744.Google Scholar
4. Krull, W., “Über einen Haupsatz der allgemeinen Idealtheorie”, S. B. Heidelberg. Akad. Wiss., Abhandl., 2 (1924), 11–16.Google Scholar
5. Krull, W., “Über Laskersche Ringe”, Rend. Circ. Mat. Palermo, Ser. 2, 7 (1958), 155–165.CrossRefGoogle Scholar
6. Mori, S., “Über allgemeine Multiplikationsringe II”, J. Sci. Hiroshima Univ., Ser. A, 4 (1934), 99–109.Google Scholar
7. Nakano, N., “Idealtheorie in einem speziellen unendlichen algebraischen Zahlkörper”, J. Sci. Hiroshima Univ., Ser. A, 16 (1952), 425–439.Google Scholar
8. Nakano, N., “Über idempotente Ideale in unendlichen algebraisohen Zahlkörpern”, J. Sci. Hiroshima Univ., Ser. A, 17 (1953), 11–20.Google Scholar
9. Nakano, N. “Über die kürzeste Darstellung der Ideale im unendlichen algobraischen Zahlkörper”, J. Sci. Hiroshima Univ., Ser. A, 17 (1953), 21–25.Google Scholar
10. Nakano, N., Über die Produkte und Quotienten von Idealen in unendlichen algebraischen Zahlkörperm”, J. Sci. Hiroshima Univ., Ser. A, 19 (1956), 239–253.Google Scholar
11. Stone, M. H., “The theory of representations for Boolean algebras”, Trans. American Math. Soc., 40 (1936), 37-111.Google Scholar
12. Zariski, O. and Samuel, P., Commutative algebra, vol. I (Van Nostrand Company, 1958).Google Scholar