Article contents
On Construction of Saturated Distinguished Chains
Published online by Cambridge University Press: 21 December 2009
Abstract
Let υ be a Henselian valuation of arbitrary rank of a field K, and let ῡ be the (unique) extension of v to a fixed algebraic closure 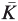 of K. For an element α ∈
of K. For an element α ∈ 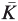 \K, a chain α = α0, α1,…,αr of elements of
\K, a chain α = α0, α1,…,αr of elements of 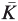 , such that αi is of minimum degree over K with the property that ῡ(αi−1 − αi) = sup{ῡ(αi−1 − β) | [K (β) : K] < [K (αi−1) : K]} and that αr ∈ K, is called a saturated distinguished chain for α with respect to (K, υ). The notion of a saturated distinguished chain has been used to obtain results about the irreducible polynomials over any complete discrete rank one valued field K and to determine various arithmetic and metric invariants associated to elements of
, such that αi is of minimum degree over K with the property that ῡ(αi−1 − αi) = sup{ῡ(αi−1 − β) | [K (β) : K] < [K (αi−1) : K]} and that αr ∈ K, is called a saturated distinguished chain for α with respect to (K, υ). The notion of a saturated distinguished chain has been used to obtain results about the irreducible polynomials over any complete discrete rank one valued field K and to determine various arithmetic and metric invariants associated to elements of 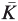 (cf. [J. Number Theory, 52 (1995), 98–118.] and [J. Algebra, 266 (2003), 14–26]). In this paper, a method is described of constructing a saturated distinguished chain for α, and also determining explicitly some invariants associated to α, when the degree of the extension K (α)/K is not divisible by the characteristic of the residue field of υ.
(cf. [J. Number Theory, 52 (1995), 98–118.] and [J. Algebra, 266 (2003), 14–26]). In this paper, a method is described of constructing a saturated distinguished chain for α, and also determining explicitly some invariants associated to α, when the degree of the extension K (α)/K is not divisible by the characteristic of the residue field of υ.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 2007
References
- 4
- Cited by


