Article contents
On certain infinite products II
Published online by Cambridge University Press: 26 February 2010
Extract
Given a sequence a(l), a(2), a(3), … of complex numbers such that a(n) ≤ 0(nc) for some c > 0, we define, for Im(z) > 0,
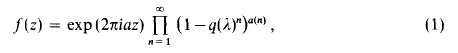
where q(λ) = exp (2πiz/λ), λ > 0 and a is a real number. Throughout this paper, for complex numbers x, w with x ≠ 0, xw = exp (w log x) and the principal branch is taken for the logarithm. Then it is easily verified that the infinite product converges absolutely and uniformly in every compact subset of the upper half plane H. Hence f(z) is holomorphic in H. The aim of this paper is to determine holomorphic functions in H defined by (1) which satisfy the special transformation formula

for some real number k under certain assumptions.
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1984
References
- 1
- Cited by


