Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T18:52:21.628Z Has data issue: false hasContentIssue false
  • English
  • Français

On asymmetry classes of convex bodies

Part of: General convexity

Published online by Cambridge University Press:  26 February 2010

Rolf Schneider
Rolf Schneider
Affiliation:
Albert-Ludwigs-Universität, Freiburg.
Get access

Extract

Asymmetry classes of convex bodies have been introduced and investigated by G. Ewald and G. C. Shephard [2], [3], [6]. These classes are defined as follows. Let 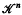denote the set of all convex bodies in n-dimensional Euclidean space ℝn. For K1, K2 ∊ 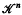write K1 ∼ K2 if there exist centrally symmetric convex bodies S1, S2 ∊ 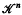such that

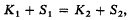
where + denotes Minkowski addition. Then ∼ is an equivalence relation on 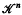and the corresponding classes are called asymmetry classes. The asymmetry class which contains K is denoted by [K].

MSC classification

Secondary: 52A20: Convex sets in $n$ dimensions (including convex hypersurfaces)
Type
Research Article
Information
Mathematika , Volume 21 , Issue 1 , June 1974 , pp. 12 - 18
Copyright
Copyright © University College London 1974

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Busemann, H.. Convex surfaces (Interscience Publ.: New York, 1958).Google Scholar
2.Ewald, G.. “Von Klassen konvexer Körper erzeugte Hilberträume”, Math. Ann., 162 (1965), 140–146.CrossRefGoogle Scholar
3.Ewald, G. and Shephard, G. C.. “Normed vector spaces consisting of classes of convex sets”, Math. Zeitschr., 91 (1966), 1–19.CrossRefGoogle Scholar
4.Schneider, R.. “Summanden konvexer Körper”, Arch. Math., 25 (1974), 83–85.CrossRefGoogle Scholar
5.Shephard, G. C.. “Decomposable convex polyhedra”, Mathematika, 10 (1963), 89–95.CrossRefGoogle Scholar
6.Shephard, G. C.. “A pre-Hilbert space consisting of classes of convex sets”, Israel J. Math., 4 (1966), 1–10.CrossRefGoogle Scholar