Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T19:01:36.029Z Has data issue: false hasContentIssue false
  • English
  • Français

On a problem of hardy and ramanujan

Published online by Cambridge University Press:  26 February 2010

P. D. T. A. Elliott
P. D. T. A. Elliott
Affiliation:
Boulder, Colorado, U.S.A.
Get access

Extract

Some sixty years ago Hardy and Ramanujan [6]introduced the notion of normal order of an arithmetic function.

A real-valued arithmetic function f)n) is said to have a normal order if there is a function g(n), which is non-negative and non-decreasing for all sufficiently large integers n, so that, for each fixed ε > 0, the integers n, for which the inequality

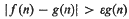
is satisfied, have asymptotic density zero. Thus, in this certain sense, f(n) behaves almost surely like g(n). We say that f(n) has the normal order g(n). In their original paper Hardy and Ramanujan asked that the function g(n) be “elementary”, but this is a requirement that subsequent researchers have dropped.

Type
Research Article
Information
Mathematika , Volume 23 , Issue 1 , June 1976 , pp. 10 - 17
Copyright
Copyright © University College London 1976

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Birch, B. J.. “Multiplicative functions with non-decreasing normal order”, Journ. London Math. Soc., 42 (1967), 149–151.CrossRefGoogle Scholar
2.Elliott, P. D. T. A.. “A conjecture of Narkiewicz.”Google Scholar
3.Elliott, P. D. T. A.. “The law of large numbers for additive arithmetic functions”, Math. Proc. Camb. Phil. Soc., 77 (1975), 33–71.CrossRefGoogle Scholar
4.Elliott, P. D. T. A.. “Sur les fonctions arithmétiques additives”, C.R. Acad. Sci. Paris, 278 (1974), 1573–1575.Google Scholar
5.Elliott, P. D. T. A.. “On connections between the Turán-Kubilius inequality and the Large Sieve: Some applications”, Amer. Math. Soc. Symposia, Vol. 24 (1973), 77–82.Google Scholar
6.Hardy, G. H. and Ramanujan, S.. “The normal number of prime factors of a number n”, Quart. J. Math., 48 (1917), 76–92.Google Scholar
7.Hardy, G. H. and Wright, E. M.. An Introduction to the Theory of Numbers, fourth edition (Oxford University Press, Oxford, 1960).Google Scholar
8.Narkiewicz, W.. “On additive functions with a non-decreasing normal order”, Colloquium Math., 32 (1974), 137–142.CrossRefGoogle Scholar
9.Norton, Karl K.. “On the number of restricted prime factors of an integer, II.”Google Scholar
10.Segal, S. L.. “A note on normal order and the Euler ø-function”, J. London Math. Soc., 39 (1964), 400–404.CrossRefGoogle Scholar
11.Segal, S. L.. “On non-decreasing normal orders”, J. London Math. Soc., 40 (1965), 459–466.CrossRefGoogle Scholar
12.Turan, P.. “On a theorem of Hardy and Ramanujan”, J. London Math. Soc., 9 (1934), 274–276.CrossRefGoogle Scholar