Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-26T17:36:06.125Z Has data issue: false hasContentIssue false
  • English
  • Français

On a problem of Granville and Zhu Regarding Pascal's triangle

Part of: Sequences and sets

Published online by Cambridge University Press:  26 February 2010

Yossi Moshe
Yossi Moshe
Affiliation:
Department of Mathematics, Ben-Gurion University of the Negev, Beer-Sheva 84105, Israel. E-mail: [email protected]
Get access

Abstract

Let A⊆ℕ, let p be a prime and w a word over ℤ pℤ ending with a non-zero digit. The relationship is investigated between the density of A. the length of w and the density of the set of numbers n for which the base p expansion of 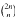ends with w0n for some a ∈ A. Also considered is the analogous problem on Pascal's triangle. This leads in particular to answering a question of Granville and Zhu [7] regarding the asymptotic frequency of sums of 3 squares in Pascal's triangle.

MSC classification

Secondary: 11B65: Binomial coefficients; factorials; $q$-identities
Type
Research Article
Information
Mathematika , Volume 51 , Issue 1-2 , December 2004 , pp. 63 - 82
Copyright
Copyright © University College London 2004

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Allouche, J. P., Gouyou-Beauchamps, D. and Skordev, G.. Transcendence of binomial and Lucas’ formal power series. J. Algebra, 210 (1998), 577–592.Google Scholar
1a.Barat, G. and Grabner, P. J.. Distribution of binomial coefficients and digital functions. J. London Math. Soc., (2) 64 (2001), 523–547.CrossRefGoogle Scholar
2.Barholosi, D. and Grabner, P. J.. Distribution des coefficients multinomiaux et q-binomiaux modulo p. Indag. Math. (N.S.), 7 (1996), 129–135.Google Scholar
3.Berend, D. and Harmse, J. E.. On some arithmetical properties of middle binomial coefficients. Acta Arith., 84 (1998), 31–41.CrossRefGoogle Scholar
4.Erdös, P.. On some divisibility properties of . Canad. Math. Bull., 1 (1964), 513–518.CrossRefGoogle Scholar
5.Furstenberg, H.. Recurrence in Ergodic Theory and Combinatorial Number Theory. Princeton University Press (1981).CrossRefGoogle Scholar
6.Granville, A. and Ramare, O.. Explicit bounds on exponential sums and the scarcity of squarefree binomial coefficients. Mathematika, 43 (1996), 73–107.Google Scholar
7.Granville, A. and Zhu, Y.. Representing binomial coefficients as sums of squares. Amer. Math. Monthly, 97 (1990), 486–493.Google Scholar
8.Kriger, N.. Arithmetical Properties of some Sequences of Binomial Coefficients. M. Sc. Thesis. Ben-Gurion University (2001).Google Scholar
9.Kummer, E.. Über die Ergänzungssätze zu den allgemainen Reciprocitätsgesetzen. J. reinc angew. Math., 44 (1852), 93–146.Google Scholar