Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
NUNOGAKI, Masanobu
AKIMUNE, Hideo
and
KAWANISHI, Masaharu
1979.
New Method of Large-Area DC Ion Beam Formation with Multiple Electron Beams, (I).
Journal of Nuclear Science and Technology,
Vol. 16,
Issue. 7,
p.
459.


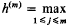 h
h