Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-27T03:57:23.060Z Has data issue: false hasContentIssue false
  • English
  • Français

The number of polytopes, configurations and real matroids

Part of: General convexity

Published online by Cambridge University Press:  26 February 2010

Noga Alon
Noga Alon
Affiliation:
Department of Mathematics, Tel Aviv University, Ramat Aviv, Israel 69978.
Get access

Abstract

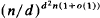We show that the number of combinatorially distinct labelled d-polytopes on n vertices is at most , as n/d → ∞. A similar bound for the number of simplicial polytopes has previously been proved by Goodman and Pollack. This bound improves considerably the previous known bounds. We also obtain sharp upper and lower bounds for the numbers of real oriented and unoriented matroids with n elements of rank d. Our main tool is a theorem of Milnor and Thorn from real algebraic geometry.

MSC classification

Secondary: 52A37: Other problems of combinatorial convexity
Type
Research Article
Information
Mathematika , Volume 33 , Issue 1 , June 1986 , pp. 62 - 71
Copyright
Copyright © University College London 1986

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

AFRAlon, N., Frankl, P. and Rödl, V.. Geometrical realization of set systems and probabilistic communication complexity. Proc. 26th FOCS, Portland, 1985, IEEE, 277–280.Google Scholar
AS1Altshuler, A. and Steinberg, L.. The complete enumeration of the 4-polytopes and 3-spheres with eight vertices. Pacific J. Math., 117 (1985), 1–16.CrossRefGoogle Scholar
AS2Altshuler, A. and Steinberg, L.. Enumeration of the quasisimplicial 3-spheres and 4-polytopes with eight vertices. Pacific J. Math. To appear.Google Scholar
BrBrückner, M.. Vielecke and Vielflache (Leipzig, 1900).Google Scholar
GP1Goodman, J. E. and Pollack, R.. Multidimensional sorting. SIAM J. Comp., 12 (1983), 484–507.CrossRefGoogle Scholar
GP2Goodman, J. E. and Pollack, R.. Upper bounds for configurations and polytopes in R d. To appear in Discrete and Computational Geometry.Google Scholar
GrGrünbaum, B.. Convex Polytopes (Wiley-Interscience, London, 1967).Google Scholar
GraGrace, D. W.. Computer search for nonisomosphic convex polyhedra. Report CS15 (Computer Science Dep., Stanford Univ., 1965).Google Scholar
GSGrünbaum, B. and Sreedharan, V. P.. An enumeration of simplicial 4 polytopes with 8 vertices. J. Combinational Theory, 2 (1967), 437–465.Google Scholar
HeHermes, O., Die formen der Vielflache. J. Reine Angew. Math., 120 (1899), 27–59, 305–353; 122 (1900), 124–154; 123 (1901), 312–342.Google Scholar
KKalai, G.. Many triangulated spheres. In preparation.Google Scholar
KlKlee, V. L.. The number of vertices of a convex polytope. Can. J. Math., 16 (1964), 701–720.Google Scholar
LlLloyd, E. K.. The number of d-polytopes with d + 3 vertices. Mathematika, 17 (1970), 120–132.CrossRefGoogle Scholar
KnKnuth, D. E.. The asymptotic number of geometries. J. Combinatorial Theory A, 17 (1974), 398–401.CrossRefGoogle Scholar
MMcMullen, P.. The maximum numbers of faces of a convex polytope. Mathematika, 17 (1970), 179–184.CrossRefGoogle Scholar
MiMilnor, J.. On the Betti numbers of real varieties. Proc. Amer. Math. Soc., 15 (1964), 275–280.Google Scholar
MoMotzkin, T. S.. Comonotone curves and polyhedra, Abstract 111. Bull. Amer. Math. Soc., 63 (1957), 35.Google Scholar
RWRichmond, L. and Wormald, N.. The asymptotic number of convex polyhedra. Trans. Amer. Math. Soc., 273 (1982), 721–735.CrossRefGoogle Scholar
ShShemer, I.. Neighborly polytopes. Israeli Math., 43 (1982), 291–314.CrossRefGoogle Scholar
StStanley, R. P.. The upper bound conjecture and Cohen-Macauley rings. Studies in Applied Math., 54 (1975), 135–142.Google Scholar
SteSteinitz, E.. Polyeder and Raumeninteilungen. Enzykl. Math. Wiss., Vol. 3 (Geometrie), Part 3AB12 (1922), 1–139.Google Scholar
ThThorn, R.. Sur l'homologie des varietes algebriques reelles. Differential and Combinational Topology, Ed. Cairns, S. S. (Princeton Univ. Press, 1965).Google Scholar
TuTutte, W. T.. A new branch of enumerative graph theory. Bull Amer. Math. Soc., 68 (1962), 500–504.CrossRefGoogle Scholar
WeWelsh, D. J. A.. Matroid Theory (Academic Press, London and New York, 1976).Google Scholar