Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-26T17:26:58.175Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on Thue's theorem

Published online by Cambridge University Press:  26 February 2010

H. Davenport
H. Davenport
Affiliation:
Trinity College, Cambridge
Get access

Extract

If θ is a real algebraic number of degree r ≥ 2, there is a computable number c = c(θ) > 0 such that

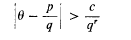
for all rational numbers p/q (q > 0). This follows directly from the definition of an algebraic number, as was shown by Liouville in 1843; and if r = 2 there is no more to be said. Axel Thue was the first to prove a stronger result when r ≥ 3; he showed that if

there are at most finitely many rational numbers p/q that satisfy

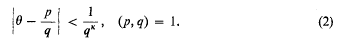
Type
Research Article
Information
Mathematika , Volume 15 , Issue 1 , June 1968 , pp. 76 - 87
Copyright
Copyright © University College London 1968

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

† “Über Annäherungswerte algebraischer Zahlen”, Journal für Math., 135 (1909), 284–305.Google Scholar

‡ Thue, loc. cit. p. 300, or Skolem, Diophantische Gleichungen (Ergebnisse der Math. V, 4), Berlin 1938, p. 95.

§ Hyyö, S., “Über die Gleichung axn−byn = z und das Catalansche Problem”, Ann. Acad. Sci. Fennicae, No. 355 (1964).Google Scholar

†† Thue asserts that it suffices for his argument if q1/q is sufficiently large, whereas in fact one needs log q1/q to be sufficiently large.

║ The first work in which this limitation of principle is overcome is that of DrBaker, A.; see his papers in Mathematika, 13 (1966), 204–216 and 14 (1967), 102–107CrossRefGoogle Scholar, and two papers to appear in Phil. Trans. Royal Soc. A. Here there is established, inter alia, the first “effective” improvement on Liouville' s inequality.

† Since the present paper was written, Schinzel has shown that a result of the type under consideration can easily be deduced from Theorem 1 of Chapter 1 of Gelfond's Transcendental and algebraic numbers, provided that r ≥ 5. See Zentralblatt für Math., 137 (1967), 258. If r ≥ 9 the result is superior to that proved in the present paper.

‡ “Über die Approximation algebraischer Zahlen,” Journal fiür Math., 175 (1936), 182–192Google Scholar, proof of Hilfssatz 3.

† Thue has n−1 instead of n in this condition, but it seems to me that n is more appropriate.

‡ Skolem, loc. cit., pp. 7–8.

† The algebra of invariants (Cambridge 1903), 375–376.Google Scholar