Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-23T19:15:14.224Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on the locally finite sum theorem

Part of: Fairly general properties

Published online by Cambridge University Press:  26 February 2010

M. K. Singal  and
Shashi Prabha Arya
M. K. Singal
Affiliation:
Meerut University, Meerut (U.P.), India.
Shashi Prabha Arya
Affiliation:
Maitreyi College, Netaji Nagar, New Delhi-23, India.
Get access

Extract

Let 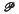be a topological property. We say that the locally finite sum theorem holds for the property 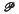if the following is true:

“If {Fα : α ∈ Λ} be a locally finite closed covering of X such that each Fα possesses the property 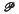, then X possesses 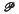.” The above property is known as the locally finite sum theorem (referred to as LFST in the present note). The LFST has been of interest to many people for it holds for many interesting properties such as metrizability, paracompactness, normality, collectionwise normality, local compactness, stratifiability, the property of being a normal M-space etc. etc. In [10], a large number of properties for which the LFST holds have been noted. In the same paper, a general method for proving this has been obtained. It has been shown that if a property 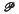is such that it is preserved under finite-to-one, closed continuous maps and also preserved under disjoint topological sums, then the LFST holds for 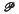and the same has been used to establish the LFST for a large number of properties. In [9,10], several interesting consequences of the LFST have been obtained. In the present note, some more interesting consequences of it have been obtained in regular, normal, collectionwise normal and countably paracompact spaces. Also, the LFST has been established for some other topological properties

MSC classification

Secondary: 54D99: None of the above, but in this section
Type
Research Article
Information
Mathematika , Volume 19 , Issue 1 , June 1972 , pp. 121 - 127
Copyright
Copyright © University College London 1972

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Dowker, C. H., “On a theorem of Hanner ”, Arkiv für Mat., 2 (1952), 307–313.CrossRefGoogle Scholar
2.Frolik, Z.,” Generalisations of compact and Lindelöf spaces ”, Czech. Math. J., 9 (1959), 172–217.CrossRefGoogle Scholar
3.Henriksen, M. and , J. R. Isbell, “Some properties of compactifications ”, Duke Math. J., 25 (1958), 83–105.CrossRefGoogle Scholar
4.Mancuiso, V. J., “Mesocompactness and related properties ”, Pacific J. Math., 33 (1970).Google Scholar
5.Michael, E., “A note on closed maps and compact sets ”, Israel J. Math., 2 (1964), 173–176.CrossRefGoogle Scholar
6.Michael, E., “No-spaces ”, J. Math. Mechanic, 15 (1966), 983–1002.Google Scholar
7.Morita, K., “Paracompactness and product spaces ”, Fund. Math., 50 (1962), 223–236.CrossRefGoogle Scholar
8.Morita, K., “Products of normal spaces with metric spaces ”, J. Math. Ann., 154 (1964), 365–382.CrossRefGoogle Scholar
9.Singal, M. K. and Arya, Shashi Prabha, “Two sum theorems for topological spaces ”, Israel J. Math., 8 (1970), 155–158.CrossRefGoogle Scholar
10.Singal, M. K. and Arya, Shashi Prabha,“More sum theorems for topological spaces ”, Unpublished.Google Scholar
11.Singal, M. K. and Deb, Mamata, “On closed mappings ”, Unpublished.Google Scholar
12.Smith, J. C., “Properties of expandable spaces ”. Presented at the Third Prague Topological Symposium, 1971.Google Scholar