Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-23T19:05:34.735Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on the integral points of a modular curve of level 7

Published online by Cambridge University Press:  26 February 2010

M. A. Kenku
M. A. Kenku
Affiliation:
Department of Mathematics, University of Lagos, Akoka, Lagos, Nigeria.
Get access

Extract

Let 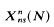. denote the modular curve associated with the normalizer of a non-split Cartan group of level N., where N. is an arbitrary integer. The curve 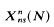is denned over Q and the corresponding scheme over ℤ[1/N] is smooth [1]. If N. is a prime, the genus formula for 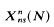. is given in [5,6]. The curve 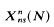. has genus 0 if N < 11 and 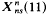has genus 1. Ligozat [5] has shown that the group of Q-rational points on 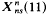has rank 1. If the genus g(N). is greater than 1, very little is known about the Q-rational points of 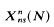. Since under simple conditions imaginary quadratic fields with class number 1 give an integral point on these curves, Serre and others have asked whether all integral points are obtained in this way [8].

Type
Research Article
Information
Mathematika , Volume 32 , Issue 1 , June 1985 , pp. 45 - 48
Copyright
Copyright © University College London 1985

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Deligne, P. and Rapoport, M.. Schémas de modules des courbes elliptiques, Vol. II of the Proceedings of the International Summer School on Modular Functions, Antwerp. (1972). Lecture Notes in Mathematics., 349 (Springer, Berlin, 1973).Google Scholar
2.Chowla, S.. Proof of a conjecture of Julia Robinson. K. norske Vidensk. Selsk. Forh., Trondheim., 34 (1961).Google Scholar
3.Klein, F.. Gesammelte mathematische Abhandlungen, Vol. 3. (Springer, Berlin, 1923).CrossRefGoogle Scholar
4.Fricke, R. and Klein, F.. Vorlesungen u'ber die Theorie der elliptischen Modulfunctionen, Vol. 3. (Chelsea).Google Scholar
5.Ligozat, G.. Courbes Modulaires de Niveau 11. Proceedings of the International Conference, University of Bonn on Modular Functions of one Variable. (1976). Lecture Notes in Mathematics., 601 (Springer, Berlin, 1977).Google Scholar
6.Mazur, B.. Rational points on modular curves. Proceedings of the International Conference, University of Bonn on Modular Functions of one Variable. (1976). Lecture Notes in Mathematics., 601 (Berlin-Heidelberg-New York, Springer, 1977).Google Scholar
7.Nagell, T.. Sur un type particuliér d'unites algébriques. Arkiv für Mat., 8 (1969), 163–184.CrossRefGoogle Scholar
8.Serre, J.-P.. Autour du théorème de Mordell-Weil. Pub. Math. U. Pierre et Marie Curie., No. 65.Google Scholar