Published online by Cambridge University Press: 26 February 2010
One may perhaps doubt whether in the geometry of numbers any particular family of lattices deserves such an attention as, for example, BCH codes receive in coding theory. However, only recently a quite interesting family has emerged. The general case of these lattices considered by Rosenbloom and Tsfasman [5, Section 2] parallels Goppa's construction of codes from algebraic curves. Here we shall take a closer look at the case of genus zero where some special features of Goppa's early codes will show up again: There is a lattice Λ (L, g) in n-dimensional euclidean space associated with a subset L of the field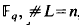 , and a polynomial g satisfying g(є) ≠ for all λ є L. For g = zd previously known sphere packings are recovered and generalized. A nonconstructive argument shows that for n → ∞ and some irreducible polynomials g Minkowski's lower packing bound is met (this being not achieved in [5] where q is fixed, but the genus grows; cf. also [4]).
, and a polynomial g satisfying g(є) ≠ for all λ є L. For g = zd previously known sphere packings are recovered and generalized. A nonconstructive argument shows that for n → ∞ and some irreducible polynomials g Minkowski's lower packing bound is met (this being not achieved in [5] where q is fixed, but the genus grows; cf. also [4]).