In 1956 Cassels proved the following result, which generalized a theorem of Marshall Hall on continued fractions. Let λ1 …, λr be any real numbers. Then there exists a real number α such that

for all integers u > 0 and for q = 1,…,r, where C = C(r) > 0. Thus all the numbers α+ λ1, …, α+ λr are badly approximable by rational numbers, which is equivalent to saying that the partial quotients in their continued fractions are bounded. In a previous paper I extended Cassels's result to simultaneous approximation. In the simplest case—that of simultaneous approximation to pairs of numbers—I proved that for any real λ1, …, λr and μ1, …, μr there exist α, β such that

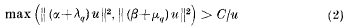
for all integers u > 0 and for q=1,…, r, where again C = C(r) > 0. Both the construction of Cassels and my extension of it to more dimensions allow one to introduce an infinity of arbitrary choices, and consequently the set of α for (1) and the set of α, β for (2) may be made to have the cardinal of the continuum.