No CrossRef data available.
Article contents
Note on a theorem of Wiener and Pitt
Published online by Cambridge University Press: 26 February 2010
Extract
Let G be a locally compact Abelian non-discrete group. Let M(G) be the convolution algebra of Radon measures on G. Let µ be an element of M(G) with its Lebesgue decomposition [1]

into absolutely continuous, purely discontinuous and continuous singular parts. The chief problem one encounters in the study of the invertibility of µ is with the case µs ≠ 0. As observed by Wiener and Pitt [2], the problem can be handled provided µs be “not too large”. In fact, Wiener and Pitt (loc. cit.) proved the following:
Let µ be a Radon measure on R (the real line) such that
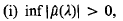
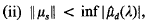
where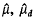 are the Fourier transforms of µ, µd, and ≑µs≑ is the variational norm of µs. Then, µ has an inverse in M (R).
are the Fourier transforms of µ, µd, and ≑µs≑ is the variational norm of µs. Then, µ has an inverse in M (R).
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1970


