Article contents
Note on a theorem of Weil-Abels
Published online by Cambridge University Press: 26 February 2010
Extract
Let G and H be Hausdorff locally compact groups. By R(G, H) we denote the space of continuous homomorphisms of G into H equipped with the compact-open topology, namely that which is generated by subsets of the form
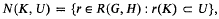
where K is any compact subset of G and U is any open subset of H. Further, let R0(G, H) be the subset of R(G, H) consisting of elements r satisfying the conditions that the quotient space H/r(G) is compact and r is proper, i.e., the action of G on H defined as the action by left translations of r(G) on H is proper. It has been shown by H. Abels [2] that if G and H are such that at least one of them has a compact defining subset then R0(G,H) is open in R(G,H). Moreover, for each r0 ∈ R0(G,H) there exists a neighbourhood M and a compact subset F of H such that r(G) F = H for all r ∈ M and for each compact subset K of H the union 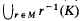 is a relatively compact subset of G. It is furthermore shown in [1] that if G contains no small subgroups and H is connected then the subset of R0(G, H) consisting of isomorphisms of G into H is open in R(G, H). These results, in the case in which H is a connected Lie Group and G is a discrete group, have been established by Weil in [5] and [6] appendix 1.
is a relatively compact subset of G. It is furthermore shown in [1] that if G contains no small subgroups and H is connected then the subset of R0(G, H) consisting of isomorphisms of G into H is open in R(G, H). These results, in the case in which H is a connected Lie Group and G is a discrete group, have been established by Weil in [5] and [6] appendix 1.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © University College London 1971
References
- 2
- Cited by


