Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-05T23:28:56.413Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on a problem of Gauthier

Published online by Cambridge University Press:  26 February 2010

Peter Lappan
Peter Lappan
Affiliation:
Michigan State University, East Lansing, Michigan 48823, U.S.A.
Get access

Extract

Let D denote the unit disc in the complex plane. If p and q are two complex numbers, let x(p, q) denote the chordal distance between p and q on the Riemann sphere. In particular, we have the formula

and

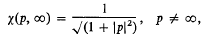
The following problem was posed by Paul Gauthier: if f(z) and g(z) are meromorphic functions in D such that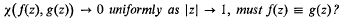 Clunie [4] has answered this problem in the negative by constructing different meromorphic functions f(z) and g(z) with the desired property. However, the functions constructed by Clunie both have an infinity of poles in D. It is the purpose of this note to give an example of two analytic functions―which thus have no poles―which also give a negative answer to the problem of Gauthier.

Type
Research Article
Information
Mathematika , Volume 18 , Issue 2 , December 1971 , pp. 274 - 275
Copyright
Copyright © University College London 1971

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bagemihl, F., Erdös, P., and Seidel, W., “Sur quelques propriétés frontieres des fonctions holomorphic définies par certains produits dans le cercle-unité ”, Ann. Ecole Norm. Sup. (3), 70 (1953), 135–147.CrossRefGoogle Scholar
Bagemihl, F. and Seidel, W., “Some remarks on boundary behaviour of analytic and meromorphic functions ”, Nagoya Math. J., 9 (1955), 69–85.CrossRefGoogle Scholar
Bieberbach, L., Lehrbuch der Funktionentheorie, 2 Aufl. Bd. II (Leipzig, Berlin, 1931).Google Scholar
Clunie, J., “On a problem of Gauthier ”, Mathematika, 18 (1971), 126–129.CrossRefGoogle Scholar
Krishnamoorthy, S., “Boundary properties of an infinite product defined in the unit-disc and a uniqueness theorem ”, Math. Zeit., 114 (1970), 93–100.CrossRefGoogle Scholar