Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T16:44:54.695Z Has data issue: false hasContentIssue false
  • English
  • Français

MOYENNES DE FONCTIONS ARITHMÉTIQUES DE FORMES BINAIRES

Part of: Diophantine equations Multiplicative number theory

Published online by Cambridge University Press:  19 January 2012

Régis de la Bretèche  and
Gérald Tenenbaum
Régis de la Bretèche
Affiliation:
Institut de Mathématiques de Jussieu, UMR 7586, Université Paris Diderot-Paris 7, UFR de Mathématiques, case 7012, Bâtiment Chevaleret, 75205 Paris Cedex 13, France (email: [email protected])
Gérald Tenenbaum
Affiliation:
Institut Élie Cartan, Université de Nancy 1, BP 239, 54506 Vandœuvre Cedex, France (email: [email protected])
Get access

Abstract

Extending classical results of Nair and Tenenbaum, we provide general, sharp upper bounds for sums of the type 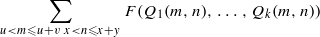where x,y,u,v have comparable logarithms, F belongs to a class defined by a weak form of sub-multiplicativity, and the Qj are arbitrary binary forms. A specific feature of the results is that the bounds are uniform within the F-class and that, as in a recent version given by Henriot, the dependency with respect to the coefficients of the Qj is made explicit. These estimates play a crucial rôle in the proof, published separately by the authors, of Manin’s conjecture for Châtelet surfaces.

Résumé

Généralisant des résultats classiques de Nair et Tenenbaum, nous fournissons des majorations générales et optimales pour des sommes du type 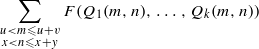où les paramètres x,y,u,v ont des logarithmes comparables, F décrit une classe de fonctions définie par une condition de sous-multiplicativité faible, et les Qj sont des formes binaires arbitraires. Ces résultats sont caractérisés par leur uniformité dans la classe des fonctions F et, à l’instar d’une version récente donnée par Henriot, une dépendance explicite en fonction des coefficients des Qj. Ces estimations jouent un rôle crucial dans la preuve, publiée séparément par les auteurs, de la conjecture de Manin pour les surfaces de Châtelet.

MSC classification

Secondary: 11N37: Asymptotic results on arithmetic functions 11N56: Rate of growth of arithmetic functions 11D45: Counting solutions of Diophantine equations
Type
Research Article
Information
Mathematika , Volume 58 , Issue 2 , July 2012 , pp. 290 - 304
Copyright
Copyright © University College London 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]de la Bretèche, R. et Browning, T. D., Sums of arithmetic functions over values of binary forms. Acta Arith. 125(3) (2006), 291–304.CrossRefGoogle Scholar
[2]de la Bretèche, R. et Browning, T. D., Binary linear forms as sums of two squares. Compos. Math. 144(6) (2008), 1375–1402.CrossRefGoogle Scholar
[3]de la Bretèche, R. et Browning, T. D., Le problème des diviseurs pour des formes binaires de degré 4. J. Reine Angew. Math. 646 (2010), 1–44.CrossRefGoogle Scholar
[4]de la Bretèche, R. et Browning, T. D., Binary forms of two squares and Châtelet surfaces. Israel J. Math. (2013), à paraître.CrossRefGoogle Scholar
[5]de la Bretèche, R., Browning, T. D. et Peyre, E., On Manin’s conjecture for a family of Châtelet surfaces. Ann. of Math. (2) 175 (2012), 1–47.CrossRefGoogle Scholar
[6]de la Bretèche, R. et Tenenbaum, G., Oscillations localisées sur les diviseurs. J. London Math. Soc. (2), à paraître.Google Scholar
[7]de la Bretèche, R. et Tenenbaum, G., Sur la conjecture de Manin pour certaines surfaces de Châtelet. Prépublication, 2011.Google Scholar
[8]Browning, T. D., Linear growth for Châtelet surfaces. Math. Ann. 346 (2010), 41–50.CrossRefGoogle Scholar
[9]Daniel, S., On the divisor-sum problem for binary forms. J. Reine Angew. Math. 507 (1999), 107–129.CrossRefGoogle Scholar
[10]Daniel, S., Uniform bounds for short sums of certain arithmetic functions of polynomial arguments. Manuscrit non publié, 2000.Google Scholar
[11]Hall, R. R. et Tenenbaum, G., Divisors (Cambridge Tracts in Mathematics 90), Cambridge University Press (Cambridge, 1988).CrossRefGoogle Scholar
[12]Henriot, K., Nair–Tenenbaum bounds uniform with respect to the discriminant. Math. Proc. Cambridge Philos. Soc., à paraître.Google Scholar
[13]Hooley, C., A new technique and its applications to the theory of numbers. Proc. London Math. Soc. (3) 38 (1979), 115–151.CrossRefGoogle Scholar
[14]Maier, H. et Tenenbaum, G., On the normal concentration of divisors. J. London Math. Soc. (2) 31 (1985), 393–400.CrossRefGoogle Scholar
[15]Maier, H. et Tenenbaum, G., On the normal concentration of divisors, 2. Math. Proc. Cambridge Philos. Soc. 147(3) (2009), 593–614.CrossRefGoogle Scholar
[16]Nagell, T., Introduction to Number Theory, 2nd edn, Chelsea Publishing Company (New York, 1964), 309 pp.Google Scholar
[17]Nair, M., Multiplicative functions of polynomial values in short intervals. Acta Arith. 62 (1992), 257–269.CrossRefGoogle Scholar
[18]Nair, M. et Tenenbaum, G., Short sums of certain arithmetic functions. Acta Math. 180 (1998), 119–144.CrossRefGoogle Scholar
[19]Peyre, E., Hauteurs et mesures de Tamagawa sur les variétés de Fano. Duke Math. J. 79 (1995), 101–218.CrossRefGoogle Scholar
[20]Shiu, P., A Brun–Titchmarsh theorem for multiplicative functions. J. Reine Angew. Math. 313 (1980), 161–170.Google Scholar
[21]Stewart, C. L., On the number of solutions of polynomial congruences and Thue equations. J. Amer. Math. Soc. 4 (1991), 793–835.CrossRefGoogle Scholar
[22]Tenenbaum, G., Sur la concentration moyenne des diviseurs. Comment. Math. Helv. 60 (1985), 411–428.CrossRefGoogle Scholar
[23]Tenenbaum, G., Introduction à la théorie analytique et probabiliste des nombres, troisième édition. Collection Échelles, Belin (2008), 592 pp.Google Scholar