Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-26T03:07:21.433Z Has data issue: false hasContentIssue false
  • English
  • Français

MORE ON LOGARITHMIC SUMS OF CONVEX BODIES

Part of: General convexity

Published online by Cambridge University Press:  10 May 2016

Christos Saroglou
Christos Saroglou*
Affiliation:
Department of Mathematics, Texas A&M University, College Station, TX 77843, U.S.A. email [email protected], [email protected]
Get access

Abstract

We prove that the log-Brunn–Minkowski inequality (log-BMI) for the Lebesgue measure in dimension $n$ would imply the log-BMI and, therefore, theB-conjecture for any even log-concave measure in dimension $n$ . As a consequence, we prove the log-BMI and the B-conjecture for any even log-concave measure in the plane. 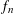Moreover, we prove that the log-BMI reduces to the following: for each dimension $n$ , there is a density $f_{n}$ , which satisfies an integrability assumption, so that the log-BMI holds for parallelepipeds with parallel facets, for the density 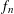$f_{n}$ . As a byproduct of our methods, we study possible log-concavity of the function 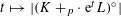$t\mapsto |(K+_{p}\cdot ~\text{e}^{t}L)^{\circ }|$ , where 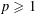$p\geqslant 1$ and 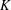$K$ , 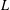$L$ are symmetric convex bodies, which we are able to prove in some instances and, as a further application, we confirm the variance conjecture in a special class of convex bodies. Finally, we establish a non-trivial dual form of the log-BMI.

MSC classification

Primary: 52A10: Convex sets in $2$ dimensions (including convex curves) 52A20: Convex sets in $n$ dimensions (including convex hypersurfaces)
Type
Research Article
Information
Mathematika , Volume 62 , Issue 3 , 2016 , pp. 818 - 841
Copyright
Copyright © University College London 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anttila, M., Ball, K. and Perissinaki, I., The central limit problem for convex bodies. Trans. Amer. Math. Soc. 355 2003, 4723–4735.CrossRefGoogle Scholar
Ball, K., Some remarks on the geometry of convex sets. In Geometric Aspects of Functional Analysis (1986/87) (Lecture Notes in Mathematics 1317 ), Springer (Berlin, 1988), 224–231.CrossRefGoogle Scholar
Bobkov, S. and Koldobsky, A., On the central limit properties of convex bodies (Lecture Notes in Mathematics 1807 ), Springer (Berlin, 2003), 44–52.Google Scholar
Borell, C., Convex measures on locally convex spaces. Ark. Mat. 12 1974, 239–252.CrossRefGoogle Scholar
Böröczky, K. J., Lutwak, E., Yang, D. and Zhang, G., The log-Brunn–Minkowski inequality. Adv. Math. 231 2012, 1974–1997.CrossRefGoogle Scholar
Böröczky, K. J., Lutwak, E., Yang, D. and Zhang, G., The logarithmic Minkowski problem. J. Amer. Math. Soc. 26 2013, 831–852.CrossRefGoogle Scholar
Böröczky, K. J., Lutwak, E., Yang, D. and Zhang, G., Affine images of isotropic measures. J. Differential Geom. accepted.Google Scholar
Bourgain, J., On the distribution of polynomials on high-dimensional convex sets. In Geometric aspects of functional analysis (1989–90) (Lecture Notes in Mathematics 1469 ), Springer (Berlin, 1991), 127–137.CrossRefGoogle Scholar
Colesanti, A. and Fragalà, I., The first variation of the total mass of log-concave functions and related inequalities. Adv. Math. 244 2013, 708–749.CrossRefGoogle Scholar
Cordero-Erausquin, D., Fradelizi, M. and Maurey, B., The (B) conjecture for the Gaussian measure of dilates of symmetric convex sets and related problems. J. Funct. Anal. 214 2004, 410–427.CrossRefGoogle Scholar
Cordero-Erausquin, D. and Gozlan, N., Transport proofs of weighted Poincaré inequalities for log-concave distributions. Preprint, 2014, arXiv:1407.3217.Google Scholar
Eldan, R., Thin shell implies spectral gap via a stochastic localization scheme. Geom. Funct. Anal. 23(2) 2013, 532–569.CrossRefGoogle Scholar
Eldan, R. and Klartag, B., Approximately gaussian marginals and the hyperplane conjecture. In Proceedings of a workshop on “Concentration, Functional Inequalities and Isoperimetry” (Contemporary Mathematics 545 ), American Mathematical Society (Providence, RI, 2011), 55–68.CrossRefGoogle Scholar
Firey, W. J., Polar means of convex bodies and a dual to the Brunn–Minkowski theorem. Canad. J. Math. 13 1961, 444–453.CrossRefGoogle Scholar
Firey, W. J., Mean cross-section measures of harmonic means of convex bodies. Pacific J. Math. 11 1961, 1263–1266.CrossRefGoogle Scholar
Fleury, B., Between Paouris concentration inequality and variance conjecture. Ann. Inst. Henri Poincaré Probab. Stat. 46(2) 2010, 299–312.CrossRefGoogle Scholar
Fradelizi, M., Guédon, O. and Pajor, A., Spherical thin-shell concentration for convex measures. Preprint.Google Scholar
Gardner, R. J., Geometric Tomography, 2nd edn., Cambridge University Press (Cambridge, 2006).CrossRefGoogle Scholar
Gardner, R. J., The Brunn–Minkowski inequality. Bull. Amer. Math. Soc. 39 2002, 355–405.CrossRefGoogle Scholar
Gardner, R. J. and Zvavitch, A., Gaussian Brunn–Minkowski inequalities. Trans. Amer. Math. Soc. 362(10) 2010, 5333–5353.CrossRefGoogle Scholar
Gardner, R. J., Hug, D., Weil, W. and Ye, D., The dual Orlicz-Brunn–Minkowski theory. Preprint, 2014.CrossRefGoogle Scholar
Guédon, O. and Milman, E., Interpolating thin-shell and sharp large-deviation estimates for isotropic log-concave measures. Geom. Funct. Anal. 21(5) 2011, 1043–1068.CrossRefGoogle Scholar
Guédon, O., Concentration phenomena in high dimensional geometry. In ESAIM Proceedings, Vol. 44 (SMAI) (2014), 47–60.Google Scholar
Hernández Cifre, M. A. and Yepes Nicolás, J., On Brunn–Minkowski type inequalities for polar bodies. J. Geom. Anal. to appear.Google Scholar
Kannan, R., Lovász, L. and Simonovits, M., Isoperimetric problems for convex bodies and a localization lemma. Discrete Comput. Geom. 13(3–4) 1995, 541–559.CrossRefGoogle Scholar
Klartag, B., On convex perturbations with a bounded isotropic constant. Geom. Funct. Anal. 16(6) 2006, 1274–1290.CrossRefGoogle Scholar
Klartag, B., A Berry-Esseen type inequality for convex bodies with an unconditional basis. Probab. Theory Related Fields 45(1) 2009, 1–33.CrossRefGoogle Scholar
Klartag, B., High-dimensional distributions with convexity properties. In Proceedings of the Fifth European Congress of Mathematics, Amsterdam, July 2008, European Mathematical Society publishing house (2010), 401–417.CrossRefGoogle Scholar
Latala, R. and Oleszkiewicz, K., Small ball probability estimate in terms of width. Studia Math. 169 2005, 305–314.CrossRefGoogle Scholar
Latala, R., On some inequalities for Gaussian measures. In Proceedings of the International Congress of Mathematicians, Beijing, Vol. II, Higher Education Press (Beijing, 2002), 813–822.Google Scholar
Livne Bar-on, A., The (B) conjecture for uniform measures in the plane. Preprint, 2013, arXiv:1311.6584.CrossRefGoogle Scholar
Lutwak, E., The Brunn–Minkowski–Firey theory. I. Mixed volumes and the Minkowski problem. J. Differential Geom. 38 1993, 131–150.Google Scholar
Lutwak, E., The Brunn–Minkowski–Firey theory. II. Affine and geominimal surface areas. Adv. Math. 118 1996, 224–294.CrossRefGoogle Scholar
Lutwak, E., Yang, D. and Zhang, G., L p affine isoperimetric inequalities. J. Differential Geom. 56 2000, 111–132.CrossRefGoogle Scholar
Lutwak, E., Yang, D. and Zhang, G., On the L p -Minkowski problem. Trans. Amer. Math. Soc. 356 2004, 4359–4370.CrossRefGoogle Scholar
Lutwak, E., Yang, D. and Zhang, G., L p John Ellipsoids. Proc. Lond. Math. Soc. 90 2005, 497–520.CrossRefGoogle Scholar
Mahler, K., Ein Minimalproblem für konvexe Polygone. Mathematica (Zutphen) B 7 1939, 118–127.Google Scholar
Marsiglietti, A., On the improvement of concavity of convex measures. Preprint, 2014, arXiv:1403.7643.Google Scholar
Milman, V. D. and Pajor, A., Isotropic position and inertia ellipsoids and zonoids of the unit ball of a normed n-dimensional space. In Geometric Aspects of Functional Analysis (1987–88) (Lecture Notes in Mathematics 1376 ), Springer (Berlin, 1989), 64–104.CrossRefGoogle Scholar
Saroglou, C., Shadow systems: remarks and extensions. Arch. Math. 100 2013, 389–399.CrossRefGoogle Scholar
Saroglou, C., Remarks on the conjectured log-Brunn–Minkowski inequality. Geom. Dedicata 2013, to appear.Google Scholar
Schneider, R., Convex Bodies: The Brunn–Minkowski Theory, 2nd edn., Cambridge University Press (Cambridge, 2014).Google Scholar
Stancu, A., The discrete planar L 0 -Minkowski problem. Adv. Math. 167 2002, 160–174.CrossRefGoogle Scholar
Stancu, A., On the number of solutions to the discrete two-dimensional L 0 -Minkowski problem. Adv. Math. 180 2003, 290–323.CrossRefGoogle Scholar
Uhrin, B., Curvilinear extensions of the Brunn–Minkowski–Lusternik inequality. Adv. Math. 109(2) 1994, 288–312.CrossRefGoogle Scholar