Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-23T19:15:48.847Z Has data issue: false hasContentIssue false
  • English
  • Français

Minkowski sums of projections of convex bodies

Part of: General convexity

Published online by Cambridge University Press:  26 February 2010

Paul Goodey
Paul Goodey
Affiliation:
Department of Mathematics, University of Oklahoma, Norman, Oklahoma 73019, U.S.A.
Get access

Abstract

If K is a convex body in 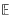d and 1≤k≤d − 1, we define Pk(K) to be the Minkowski sum or Minkowski average of all the projections of K onto k-dimensional subspaces of 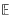d. The operator Pd − 1, was first introduced by Schneider, who showed that, if Pd − 1(K) = cK, then K is a ball. More recently, Spriestersbach showed that, if Pd − 1(K) = cK then K = M. In addition, she gave stability versions of this result and Schneider's. We will describe further injectivity results for the operators Pk. In particular, we will show that Pk is injective if k≤d/2 and that P2 is injective in all dimensions except d = 14, where it is not injective.

MSC classification

Secondary: 52A20: Convex sets in $n$ dimensions (including convex hypersurfaces)
Type
Research Article
Information
Mathematika , Volume 45 , Issue 2 , December 1998 , pp. 253 - 268
Copyright
Copyright © University College London 1998

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Chern, S. S.. On the kinematic formula in integral geometry, J. Math. Mech., 16 (1966), 101–118.Google Scholar
Fallert, H., Goodey, P. and Weil, W.. Spherical projections and centrally symmetric sets. Adv. in Math., 129 (1997), 301–322.CrossRefGoogle Scholar
Gardner, R.. Geometric Tomography (Cambridge University Press, Cambridge, 1995).Google Scholar
Goodey, P.. Radon transforms of projection functions. Proc. Camb. Phil. Soc. (To appear).Google Scholar
Goodey, P., Kiderlen, M. and Weil, W.. Section and projection means of convex bodies. Monatsh. Math. (To appear).Google Scholar
Goodey, P. and Weil, W.. The determination of convex bodies from the mean of random sections, Math. Proc. Camb. Phil. Soc, 112 (1992), 419–430.CrossRefGoogle Scholar
Goodey, P. and Weil, W.. Zonoids and generalizations, In: Handbook of Convex Geometry Gruber, P. M. and Wills, J. M., eds. (North Holland, Amsterdam, 1993), 296–317.Google Scholar
Gradshteyn, I. S., and Ryzhik, I. M.. Tables of integrals, series and products (Academic Press, San Diego, 1994).Google Scholar
Groemer, H.. Geometric Applications of Fourier Series and Spherical Harmonics (Cambridge University Press, Cambridge, 1996).CrossRefGoogle Scholar
Howard, R.. The kinematic formula in Riemannian homogeneous spaces. Mem. Amer. Math. Soc, 509 (1993).Google Scholar
Kiderlen, M.. Schnittmittelungen und kovariante Endomorphismen konvexer Korper. Ph.D. Thesis, Universitat Karlsruhe (in preparation).Google Scholar
Muller, C.. Spherical Harmonics (Springer, Berlin, 1966).CrossRefGoogle Scholar
Santalo, L. A.. Integral geometry and geometric probability (Addison-Wesley, Reading, 1976).Google Scholar
Schneider, R.. Rekonstruktion eines konvexen Korpers aus seinen Projektionen. Math. Nachr., 79 (1977), 325–329.CrossRefGoogle Scholar
Schneider, R.. Convex Bodies: The Brunn-Minkowski Theory (Cambridge University Press, Cambridge, 1993).CrossRefGoogle Scholar
Schneider, R. and Weil, W.. Zonoids and related topics. In: Convexity and its Applications Gruber, P. M. and Wills, J. M., eds. (Birkhauser, Basel, 1983), 296–317.CrossRefGoogle Scholar
Spriestersbach, K.. Determination of a convex body from the average of projections and stability results (To appear).Google Scholar
Vitale, R.. Lp metrics for compact convex sets, J. Approx. Theory, 45 (1985), 280287.Google Scholar
Weil, W.. Zonoide und verwandte Klassen konvexer Korper, Monatshefte Math., 94 (1982), 73–84.CrossRefGoogle Scholar
Weil, W.. The mean normal distribution of stationary random sets and particle processes, In: Advances in Theory and Applications of Random Sets, Proc. International Symposium, Oct. 9–11, 1996 Fontainebleau, France, Jeulin, D., ed. (World Scientific Publ., Singapore, 1997), 21–33.Google Scholar