Let q(x1; …, xn) be a positive definite quadratic form in n variables with real coefficients. Minkowski defined the successive minima of q as follows. Let S1 denote the least value assumed by q for integers x1 …, xn, not all zero, and let 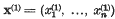be a point at which this value is attained. Let S2 denote the least value assumed by q at integral points which are not multiples of x(1), and let x(2) be such a point at which this value is attained. Let S3 be the least value of q at integral points which are not linearly dependent on x(1) and x(2), and so on. We have

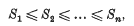
and it is easy to see that these numbers are uniquely defined, even though there may be several choices for the points x(1), …, x(n). The determinant N of the coordinates of the points x(1), …, x(n) is a non-zero integer. We denote by N (q) the least value of this integer (taken positively) for all permissible choices of the n minimal points, and by N′(q) its greatest value. Plainly N(q) and N′(q) are arithmetical invariants of q, that is, they are the same for two forms which are equivalent under a linear substitution with integral coefficients and determinant ±1.