Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T19:18:17.886Z Has data issue: false hasContentIssue false
  • English
  • Français

A METRIC THEORY OF MINIMAL GAPS

Part of: Probabilistic theory: distribution modulo $1$; metric theory of algorithms

Published online by Cambridge University Press:  21 May 2018

Zeév Rudnick
Zeév Rudnick*
Affiliation:
Raymond and Beverly Sackler School of Mathematical Sciences, Tel Aviv University, Tel Aviv 69978, Israel email [email protected]
Get access

Abstract

We study the minimal gap statistic for fractional parts of sequences of the form 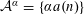${\mathcal{A}}^{\unicode[STIX]{x1D6FC}}=\{\unicode[STIX]{x1D6FC}a(n)\}$, where 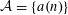${\mathcal{A}}=\{a(n)\}$ is a sequence of distinct integers. Assuming that the additive energy of the sequence is close to its minimal possible value, we show that for almost all $\unicode[STIX]{x1D6FC}$, the minimal gap 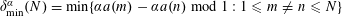$\unicode[STIX]{x1D6FF}_{\min }^{\unicode[STIX]{x1D6FC}}(N)=\min \{\unicode[STIX]{x1D6FC}a(m)-\unicode[STIX]{x1D6FC}a(n)\hspace{0.2em}{\rm mod}\hspace{0.2em}1:1\leqslant m\neq n\leqslant N\}$ is close to that of a random sequence.

MSC classification

Primary: 11K06: General theory of distribution modulo $1$
Type
Research Article
Information
Mathematika , Volume 64 , Issue 3 , 2018 , pp. 628 - 636
Copyright
Copyright © University College London 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aistleitner, C., Larcher, G. and Lewko, M., Additive energy and the Hausdorff dimension of the exceptional set in metric pair correlation problems, with an appendix by J. Bourgain. Israel J. Math. 222(1) 2017, 463–485.Google Scholar
Balog, A., Granville, A. and Solymosi, J., Gaps between fractional parts, and additive combinatorics. Q. J. Math. 68 2017, 1–12.Google Scholar
Blomer, V., Bourgain, J., Radziwiłł, M. and Rudnick, Z., Small gaps in the spectrum of the rectangular billiard. Ann. Sci. Éc. Norm. Supér. (4) 50(5) 2017, 1283–1300.Google Scholar
Bloom, T. F., Chow, S., Gafni, A. and Walker, A., Additive energy and the metric Poissonian property. Preprint, 2017, arXiv:1709.02634 [math.NT].Google Scholar
Bondarenko, A. and Seip, K., GCD sums and complete sets of square-free numbers. Bull. Lond. Math. Soc. 47(1) 2015, 29–41.Google Scholar
Dyer, T. and Harman, G., Sums involving common divisors. J. Lond. Math. Soc. 34 1986, 1–11.Google Scholar
Heath-Brown, D. R., Pair correlation for fractional parts of 𝛼n 2 . Math. Proc. Cambridge Philos. Soc. 148(3) 2010, 385–407.Google Scholar
Lachmann, T. and Technau, N., On exceptional sets in the metric Poissonian pair correlations problem, Preprint, 2017, arXiv:1708.08599.Google Scholar
Lévy, P., Sur la division d’un segment par des points choisis au hasard. C. R. Acad. Sci. Paris 208 1939, 147–149.Google Scholar
Marklof, J. and Strömbergsson, A., Equidistribution of Kronecker sequences along closed horocycles. Geom. Funct. Anal. 13 2003, 1239–1280.Google Scholar
Rudnick, Z. and Sarnak, P., The pair correlation function of fractional parts of polynomials. Comm. Math. Phys. 194(1) 1998, 61–70.Google Scholar
Rudnick, Z. and Zaharescu, A., A metric result on the pair correlation of fractional parts of sequences. Acta Arith. 89(3) 1999, 283–293.Google Scholar
Vâjâitu, M. and Zaharescu, A., Distinct gaps between fractional parts of sequences. Proc. Amer. Math. Soc. 130 2002, 3447–3452.Google Scholar
Walker, A., The primes are not metric Poissonian. Mathematika 64(1) 2018, 230–236.Google Scholar