Hyperplane mean values of non-negative subharmonic functions have been studied in many papers, of which [2] and [3] are examples. Recently, Armitage [1] began a study of hyperplane means of non-negative superharmonic functions. One of his results [1, Theorem 2] shows that, if w is a positive superharmonic function on

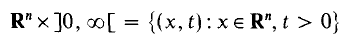
and n/(n + 1) p < 1, then

as t → ∞, while another [1, Theorem 1] shows that, if 0 < p ≤ n/(n + l), then the integral in (1) is always infinite. However, he did not present a complete analogue of the result of Flett and Brawn [2, 3], which states that, if Ф: [0, ∞ [ → [0, ∞ [ is a non-decreasing convex function such that Ф(u)/u → 0 as u → 0 +, and w is a nonnegative subharmonic function on Rn × ]0, ∞ [, then under certain conditions on the size of w, the integral mean

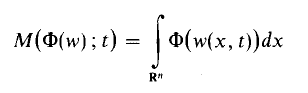
tends to zero as t → ∞. In this note we present an analogue for superharmonic functions of the above result, in which the mean M(Ф(w); t) is shown to tend to infinity with t, provided that Ф(u)/u → ∞ as u → 0 +, and which therefore generalizes (1). It might be expected that, in dealing with the superharmonic case, the function Ф would have to be concave, so that Ф(w) would also be superharmonic. It turns out that this condition is unnecessary.