Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-04T21:07:05.434Z Has data issue: false hasContentIssue false
  • English
  • Français

LOWER BOUND THEOREMS AND A GENERALIZED LOWER BOUND CONJECTURE FOR BALANCED SIMPLICIAL COMPLEXES

Part of: Polytopes and polyhedra PL-topology Algebraic combinatorics

Published online by Cambridge University Press:  01 February 2016

Steven Klee  and
Isabella Novik
Steven Klee
Affiliation:
Department of Mathematics, Seattle University, Seattle, WA 98122, U.S.A. email [email protected]
Isabella Novik
Affiliation:
Department of Mathematics, University of Washington, Seattle, WA 98195-4350, U.S.A. email [email protected]
Get access

Abstract

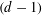A $(d-1)$-dimensional simplicial complex is called balanced if its underlying graph admits a proper 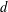$d$-coloring. We show that many well-known face enumeration results have natural balanced analogs (or at least conjectural analogs). Specifically, we prove the balanced analog of the celebrated lower bound theorem (LBT) for normal pseudomanifolds and characterize the case of equality; we introduce and characterize the balanced analog of the Walkup class; and we propose the balanced analog of the generalized lower bound conjecture (GLBC) and establish some related results. We close with constructions of balanced manifolds with few vertices.

MSC classification

Primary: 05E45: Combinatorial aspects of simplicial complexes
Secondary: 52B12: Special polytopes (linear programming, centrally symmetric, etc.) 52B70: Polyhedral manifolds 57Q15: Triangulating manifolds
Type
Research Article
Information
Mathematika , Volume 62 , Issue 2 , 2016 , pp. 441 - 477
Copyright
Copyright © University College London 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Asimow, L. and Roth, B., The rigidity of graphs. Trans. Amer. Math. Soc. 245 1978, 279–289.Google Scholar
Asimow, L. and Roth, B., The rigidity of graphs. II. J. Math. Anal. Appl. 68(1) 1979, 171–190.Google Scholar
Bagchi, B., The mu vector, Morse inequalities and a generalized lower bound theorem for locally tame combinatorial manifolds. European J. Combin. 51 2016, 69–83.Google Scholar
Bagchi, B. and Datta, B., Lower bound theorem for normal pseudomanifolds. Expo. Math. 26(4) 2008, 327–351.Google Scholar
Bagchi, B. and Datta, B., Minimal triangulations of sphere bundles over the circle. J. Combin. Theory Ser. A 115(5) 2008, 737–752.Google Scholar
Bagchi, B. and Datta, B., On k-stellated and k-stacked spheres. Discrete Math. 313(20) 2013, 2318–2329.CrossRefGoogle Scholar
Barnette, D., Graph theorems for manifolds. Israel J. Math. 16 1973, 62–72.Google Scholar
Barnette, D., A proof of the lower bound conjecture for convex polytopes. Pacific J. Math. 46 1973, 349–354.Google Scholar
Barnette, D., Decompositions of homology manifolds and their graphs. Israel J. Math. 41(3) 1982, 203–212.Google Scholar
Bayer, M. M. and Billera, L. J., Generalized Dehn–Sommerville relations for polytopes, spheres and Eulerian partially ordered sets. Invent. Math. 79(1) 1985, 143–157.Google Scholar
Billera, L. and Lee, C. W., A proof of the sufficiency of McMullen’s conditions for f-vectors of simplicial convex polytopes. J. Combin. Theory Ser. A 31(3) 1981, 237–255.Google Scholar
Björner, A., Frankl, P. and Stanley, R., The number of faces of balanced Cohen–Macaulay complexes and a generalized Macaulay theorem. Combinatorica 7(1) 1987, 23–34.Google Scholar
Browder, J. and Klee, S., Lower bounds for Buchsbaum* complexes. European J. Combin. 32 2011, 146–153.Google Scholar
Chestnut, J., Sapir, J. and Swartz, E., Enumerative properties of triangulations of spherical bundles over S 1 . European J. Combin. 29(3) 2008, 662–671.Google Scholar
Datta, B. and Murai, S., On stacked triangulated manifolds. Preprint, 2014, arXiv:1407.6767.Google Scholar
Ehrenborg, R. and Karu, K., Decomposition theorem for the cd -index of Gorenstein posets. J. Algebraic Combin. 26(2) 2007, 225–251.Google Scholar
Fogelsanger, A., The generic rigidity of minimal cycles. PhD Thesis, Cornell University, 1988 (ProQuest LLC, Ann Arbor, MI).Google Scholar
Frankl, P., Füredi, Z. and Kalai, G., Shadows of colored complexes. Math. Scand. 63(2) 1988, 169–178.Google Scholar
Goff, M., Klee, S. and Novik, I., Balanced complexes and complexes without large missing faces. Ark. Mat. 46(2) 2011, 335–350.Google Scholar
Joswig, M., Projectivities in simplicial complexes and colorings of simple polytopes. Math. Z. 240(2) 2002, 243–259.Google Scholar
Kalai, G., Rigidity and the lower bound theorem. I. Invent. Math. 88(1) 1987, 125–151.Google Scholar
Karu, K., The cd-index of fans and posets. Compositio Math. 142(3) 2006, 701–718.Google Scholar
Klee, V., A combinatorial analogue of Poincaré’s duality theorem. Canad. J. Math. 16 1964, 517–531.Google Scholar
Kubitzke, M. and Murai, S., Balanced generalized lower bound inequality for simplicial polytopes. Preprint, 2015, arXiv:1503.06430.Google Scholar
Kühnel, W., Higher-dimensional analogues of Czászár’s torus. Results Math. 9(1–2) 1986, 95–106.Google Scholar
Lutz, F., The manifold page. http://page.math.tu-berlin.de/∼lutz/stellar/.Google Scholar
Lutz, F., Triangulated manifolds with few vertices and vertex-transitive group actions. Berichte aus der Mathematik. [Reports from Mathematics]. Verlag Shaker, Aachen. Dissertation, Technischen Universität Berlin, Berlin, 1999.Google Scholar
Lutz, F., Sulanke, T. and Swartz, E., f-vectors of 3-manifolds. Electron. J. Combin. 16 2009, (2, Special volume in honor of Anders Bjorner): Research Paper 13, 33.Google Scholar
McMullen, P., Triangulations of simplicial polytopes. Beiträge Algebra Geom. 45(1) 2004, 37–46.Google Scholar
McMullen, P. and Walkup, D. W., A generalized lower-bound conjecture for simplicial polytopes. Mathematika 18 1971, 264–273.Google Scholar
Munkres, J., Topological results in combinatorics. Michigan Math. J. 31(1) 1984, 113–128.Google Scholar
Murai, S. and Nevo, E., On the generalized lower bound conjecture for polytopes and spheres. Acta. Math. 210 2013, 185–202.Google Scholar
Murai, S. and Nevo, E., On r-stacked triangulated manifolds. J. Algebraic Combin. 39(2) 2014, 373–388.CrossRefGoogle Scholar
Murai, S., Tight combinatorial manifolds and graded betti numbers. Collect. Math. 66 2015, 367–386, doi:10.1007/s13348-015-0137-z.Google Scholar
Novik, I. and Swartz, E., Socles of Buchsbaum modules, complexes and posets. Adv. Math. 222(6) 2009, 2059–2084.Google Scholar
Stanley, R. P., Balanced Cohen–Macaulay complexes. Trans. Amer. Math. Soc. 249(1) 1979, 139–157.Google Scholar
Stanley, R. P., The number of faces of a simplicial convex polytope. Adv. Math. 35(3) 1980, 236–238.Google Scholar
Stanley, R. P., Flag f-vectors and the cd-index. Math. Z. 216(3) 1994, 483–499.Google Scholar
Stanley, R. P., Combinatorics and Commutative Algebra, 2nd edn., Birkhäuser (Boston, 1996).Google Scholar
Steenrod, N. E., The classification of sphere bundles. Ann. of Math. (2) 45 1944, 294–311.CrossRefGoogle Scholar
Swartz, E., g-elements, finite buildings and higher Cohen–Macaulay connectivity. J. Combin. Theory Ser. A 113(7) 2006, 1305–1320.Google Scholar
Swartz, E., Topological finiteness for edge-vertex enumeration. Adv. Math. 219(5) 2008, 1722–1728.Google Scholar
Swartz, E., Face enumeration—from spheres to manifolds. J. Eur. Math. Soc. (JEMS) 11(3) 2009, 449–485.Google Scholar
Tay, T.-S., Lower-bound theorems for pseudomanifolds. Discrete Comput. Geom. 13(2) 1995, 203–216.Google Scholar
Walkup, D., The lower bound conjecture for 3- and 4-manifolds. Acta Math. 125 1970, 75–107.Google Scholar
Whiteley, W., Some matroids from discrete applied geometry. In Matroid Theory (Seattle, WA, 1995) (Contemporary Mathematics 197 ), American Mathematical Society (Providence, RI, 1996), 171–311.Google Scholar
Zheng, H., Minimal balanced triangulations of sphere bundles over the circle. Preprint, 2015, arXiv:1505.05598.Google Scholar