Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-23T19:40:09.167Z Has data issue: false hasContentIssue false
  • English
  • Français

Local cohomology and modules of generalized fractions

Part of: Local rings and semilocal rings

Published online by Cambridge University Press:  26 February 2010

R. Y. Sharp  and
H. Zakeri
R. Y. Sharp
Affiliation:
Department of Pure Mathematics, The University, Sheffield. S3 7RH
H. Zakeri
Affiliation:
Department for Teacher Education, 49 Mobarezan Avenue, Tehran, Iran.
Get access

Extract

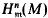The purpose of this paper is to provide additional evidence to support our view that the modules of generalized fractions introduced in [8] are worth further investigation: we show that, for a module M over a (commutative, Noetherian) local ring A (with identity) having maximal ideal m and dimension n, the n-th local cohomology module may be viewed as a module of generalized fractions of M with respect to a certain triangular subset of An + 1, and we use this work to formulate Hochster's ‘Monomial Conjecture’ [2, Conjecture 1]; in terms of modules of generalized fractions and to make a quick deduction of one of Hochster's results which supports that conjecture.

MSC classification

Secondary: 13H99: None of the above, but in this section
Type
Research Article
Information
Mathematika , Volume 29 , Issue 2 , December 1982 , pp. 296 - 306
Copyright
Copyright © University College London 1982

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Grothendieck, A.. Local cohomology, Lecture Notes in Mathematics 41 (Springer, Berlin, 1967).Google Scholar
2.Hochster, M.. Contracted ideals from integral extensions of regular rings. Nagoya Math. J., 51 (1973), 2543.CrossRefGoogle Scholar
3.Hochster, M.. Topics in the homological theory of modules over commutative rings, Conference Board of the Mathematical Sciences Regional Conference Series in Mathematics 24 (American Mathematical Society, Providence, 1975).CrossRefGoogle Scholar
4.Hochster, M.. Associated graded rings derived from integrally closed ideals and the local homological conjectures. Preprint, University of Michigan, 1981.Google Scholar
5.Macdonald, I. G. and Sharp, R. Y.. An elementary proof of the non-vanishing of certain local cohomology modules. Quart. J. Math. Oxford (2), 23 (1972), 197–204.CrossRefGoogle Scholar
6.Northcott, D. G.. Ideal theory (Cambridge University Press, Cambridge, 1953).CrossRefGoogle Scholar
7.Sharp, R. Y.. Local cohomology theory in commutative algebra1. Quart. J. Math. Oxford (2), 21 (1970), 425–434.CrossRefGoogle Scholar
8.Sharp, R. Y. and Zakeri, H.. Modules of generalized fractions. Mathematika, 29 (1982), 32–41.CrossRefGoogle Scholar