Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Vinogradov, A. I.
and
Sprindzhuk, V. G.
1968.
On representation of numbers by binary forms.
Mathematical Notes of the Academy of Sciences of the USSR,
Vol. 3,
Issue. 4,
p.
235.
1968.
Contributions to the theory of diophantine equations I. On the representation of integers by binary forms.
Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences,
Vol. 263,
Issue. 1139,
p.
173.
Baker, A.
1968.
Linear forms in the logarithms of algebraic numbers (IV).
Mathematika,
Vol. 15,
Issue. 2,
p.
204.
Amice, Yvette
1971.
Séminaire Bourbaki vol. 1970/71 Exposés 382–399.
Vol. 244,
Issue. ,
p.
1.
Baker, A
Birch, B.J
and
Wirsing, E.A
1973.
On a problem of Chowla.
Journal of Number Theory,
Vol. 5,
Issue. 3,
p.
224.
Waldschmidt, Michel
1973.
Solution du huitième problème de Schneider.
Journal of Number Theory,
Vol. 5,
Issue. 3,
p.
191.
Tijdeman, R.
1973.
An auxiliary result in the theory of transcendental numbers.
Journal of Number Theory,
Vol. 5,
Issue. 1,
p.
80.
Masser, D. W.
1982.
A vanishing theorem for power series.
Inventiones Mathematicae,
Vol. 67,
Issue. 2,
p.
275.
Wolfart, J.
1983.
Eine arithmetische Eigenschaft automorpher Formen zu gewissen nicht-arithmetischen Gruppen.
Mathematische Annalen,
Vol. 262,
Issue. 1,
p.
1.
Shorey, T.N
1983.
Divisors of convergents of a continued fraction.
Journal of Number Theory,
Vol. 17,
Issue. 1,
p.
127.
Chandrasekaran, R.
and
Tamir, A.
1984.
Polynomial testing of the query “IS ab ≥ cd?” with application to finding a minimal cost reliability ratio spanning tree.
Discrete Applied Mathematics,
Vol. 9,
Issue. 2,
p.
117.
Hazewinkel, M.
1988.
Encyclopaedia of Mathematics.
p.
1.
Vinogradova, I. A.
El’kin, A. G.
Prokhorov, Yu. V.
Efimov, B. A.
Kuptsov, L. P.
Rozov, N. Kh.
Oskolkov, V. A.
Kudryavtsev, L. D.
Khvedelidze, B. V.
Zakharov, A. A.
Tsalenko, M. Sh.
Solomentsev, E. D.
Ershov, Yu. L.
Dolgachev, I. V.
Venkov, B. B.
Parshin, A. N.
Kostrikin, A. I.
Ivanov, A. B.
Terekhin, A. P.
Emelyanov, V. F.
Sazonov, V. V.
Voĭtsekhovskiĭ, M. I.
Volkov, I. I.
Aleksandrov, P. S.
Prokhorov, A. V.
Zubkov, A. M.
Grishin, V. N.
Danilevich, A. A.
Nagornyĭ, N. M.
D’yakonov, E. G.
Ikramov, Kh. D.
Bakhvalov, N. S.
Arkhangel’skiĭ, A. V.
Rumyantsev, V. V.
Zarelua, A. V.
Mal’tsev, A. A.
Ivanova, O. A.
Fedotov, V. P.
Kubilyus, I. P.
Bredikhin, B. M.
Dobrushin, P. L.
Prelov, V. V.
Mikhalev, A. V.
Andrunakievich, V. A.
Fedorchuk, V. V.
Platonov, V. P.
Favorskiĭ, A. P.
Anosov, D. V.
Danilov, V. I.
Tonkov, E. L.
Onishchik, A. L.
Pigolkina, T. S.
Pogolkina, T. S.
Skornyakov, L. A.
Sobolev, V. I.
Sabitov, I. Kh.
Lebedev, V. I.
Lykov, A. V.
Dorodnitsyn, A. A.
Iskovskikh, V. A.
Lumiste, Ü.
Shirokov, A. P.
Parkhomenko, A. S.
Shikin, E. V.
Zalgaller, V. A.
Fedoryuk, M. V.
Samarin, M. K.
Germogenova, T. A.
Sklyarenko, E. G.
Chogoshvili, G. S.
Chernavskiĭ, A. V.
Ershov, A. P.
Lutsikovich, V. V.
Merzlyakov, Yu. I.
Shirshov, A. I.
Remeslennikov, V. N.
Gorin, E. A.
Kudryavtsev, V. B.
Gaĭnov, A. T.
Latyshev, V. N.
Voskresenskiĭ, V. E.
Proskuryakov, I. V.
Zhizhchenko, A. B.
Platonov, K. P.
Shidlovskiĭ, A. B.
Galochkin, A. I.
Nemytov, A. I.
Fofanova, T. S.
Vinogradov, A. I.
Baranovich, T. M.
Subbotin, Yu. N.
Smirnov, D. M.
Novikov, S. P.
Iskhovskikh, V. A.
Martynyuk, V. V.
Uspenskiĭ, V. A.
Barzdin, Ya. M.
Petri, N. V.
Zhuravlev, Yu. I.
Adyan, S. I.
Muchnik, A. A.
Alekseevskiĭ, D. V.
Bityutskov, V. I.
Bredikhina, E. A.
Zhikov, V. V.
Levitan, B. M.
Millionshchikov, V. M.
Vil’yams, N. N.
Vrublevskaya, I. N.
Zhevlakov, K. A.
Bokut, L. A.
Romanovskiĭ, N. S.
Vitushkin, A. G.
Chirka, E. M.
Kutuzov, B. V.
Gonchar, A. A.
Shabat, B. V.
Poznyak, E. G.
Popov, V. L.
Ponomarev, D. A.
Gladkiĭ, A. V.
Karatsuba, A. A.
Zabreĭko, P. P.
Zhelobenko, D. P.
Kirillov, A. A.
Leontovich-Andronova, E. A.
Prudnikov, A. P.
Sidorov, L. A.
Minlos, R. A.
Dragalin, A. G.
Bazylev, V. T.
Kaz’min, Yu. A.
Sretenskiĭ, L. N.
Korneĭchuk, N. I.
Motornyĭ, V. P.
Ryaben’kiĭ, V. S.
Korneĭchuk, N. P.
Dolzhenko, E. P.
Konovalov, V. N.
Vilkas, E. I.
Kokorin, A. I.
Kopytov, V. M.
Shevrin, L. N.
Sokolov, D. D.
Rogozin, B. A.
Burago, Yu. D.
Lebedev, N. A.
Bukhshtab, A. A.
Pechaev, V. I.
Mints, G. E.
Klimov, N. I.
Mikheev, V. M.
Shunkov, V. P.
Golubov, B. I.
Leont’ev, A. F.
Nagornyi, N. M.
Nesterov, V. V.
Podobed, V. V.
Erpylev, N. P.
Minin, I. N.
Latyshev, K. P.
Shabunin, M. I.
Gavrilov, V. I.
Shalaevskiĭ, O. V.
Bogdanov, Yu. S.
Butenin, N. V.
Yanov, Yu. I.
Kydryavtsev, V. B.
Red’ko, V. N.
Madatyan, Kh. A.
Letichevskiĭ, A. A.
Buevich, V. A.
Aleshin, S. V.
Letov, A. M.
Fitialov, S. Ya.
Andrianov, A. N.
Kuzichev, A. S.
Plechko, V. N.
Grebenikov, E. A.
Novikov, P. S.
Kabakov, F. A.
and
Taĭmanov, A. D.
1995.
Encyclopaedia of Mathematics.
p.
1.
Conway, John H.
and
Guy, Richard K.
1996.
The Book of Numbers.
p.
237.
Lamzouri, Youness
2007.
On the number of linear forms in logarithms.
Journal of Number Theory,
Vol. 125,
Issue. 1,
p.
247.
Алексенцев, Юрий Михайлович
and
Aleksentsev, Yurii Mikhailivich
2008.
Многочлен Гильберта и линейные формы от логарифмов алгебраических чисел.
Известия Российской академии наук. Серия математическая,
Vol. 72,
Issue. 6,
p.
5.
Xia, Bican
and
Zhang, Zhihai
2010.
Termination of linear programs with nonlinear constraints.
Journal of Symbolic Computation,
Vol. 45,
Issue. 11,
p.
1234.
Guan, Daniel
2011.
On classification of compact complex solvmanifolds.
Journal of Algebra,
Vol. 347,
Issue. 1,
p.
69.
Narkiewicz, Władysław
2012.
Rational Number Theory in the 20th Century.
p.
307.
Guan, Daniel
2013.
Toward a classification of real compact solvmanifolds with real symplectic structures.
Journal of Algebra,
Vol. 379,
Issue. ,
p.
144.
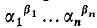 is transcendental.
is transcendental.

