Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T19:12:19.272Z Has data issue: false hasContentIssue false
  • English
  • Français

Least primitive roots modulo the square of a prime ideal

Published online by Cambridge University Press:  26 February 2010

Jürgen G. Hinz
Jürgen G. Hinz
Affiliation:
Department of Mathematics, University of Marburg, Lahnberge, D-3550 Marburg, Federal Republic of Germany.
Get access

Extract

Let K be an algebraic number field of degree n = r1 + 2r2 (in the usual notation) over the rationals. ZK will denote the ring of integers in K. Consider the set of all totally positive primitive roots modulo the square of a prime ideal p of first degree in K. We recall (see e.g., [6], p. 249) that there exists such a primitive root mod p2, if, and only if, p is of first degree. Let vp be a least element of this set, least in the sense that its norm Nvp is minimal. We ask for the order of magnitude of Nvp in comparison to Np2. The author”s work [5] on cubefree ideal modulus character sums yields the estimate

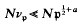
for any a > 0, where the implied «-constant depends on a and K.

Type
Research Article
Information
Mathematika , Volume 33 , Issue 2 , December 1986 , pp. 244 - 251
Copyright
Copyright © University College London 1986

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Burgess, D.A.. The average of the least primitive root modulo p2. Acta Arith., 18(1971), 263–271.Google Scholar
2.Cohen, S. D., Odoni, R. W. K. and Stothers, W. W.. On the least primitive root modulo p2. Bull. London Math. Soc., 6 (1974), 42–46.Google Scholar
3.Hinz., J. G., Character sums and primitive roots in algebraic number fields. Monatshefte für Mathematik, 95 (1983), 275–286.Google Scholar
4.Hinz., J. G., The average order of magnitude of least primitive roots in algebraic number fields. Mathematika, 30 (1983), 11–25.Google Scholar
5.Hinz, J. G.. Cubefree ideal modulus character sums. Arch. Math., 46 (1986), 307–314.Google Scholar
6.Narkiewicz, W.. Elementary and analytic theory of algebraic numbers (PWN, Warszawa, 1974).Google Scholar