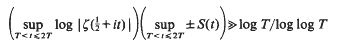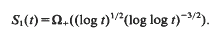Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Карацуба, Анатолий Алексеевич
Karatsuba, Anatolii Alekseevich
Королeв, Максим Александрович
and
Korolev, Maxim Aleksandrovich
2005.
Аргумент дзета-функции Римана.
Успехи математических наук,
Vol. 60,
Issue. 3,
p.
41.
Hejhal, Dennis A.
2007.
Turing: a bit off the beaten path.
The Mathematical Intelligencer,
Vol. 29,
Issue. 1,
p.
27.
Borwein, Peter
Choi, Stephen
Rooney, Brendan
and
Weirathmueller, Andrea
2008.
The Riemann Hypothesis.
p.
93.
Bondarenko, Andriy
and
Seip, Kristian
2018.
Extreme values of the Riemann zeta function and its argument.
Mathematische Annalen,
Vol. 372,
Issue. 3-4,
p.
999.
Dobner, Alexander
2024.
Large deviations of the argument of the Riemann zeta function.
Mathematika,
Vol. 70,
Issue. 3,


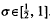 . By refining Selberg's method, we study the large values of
. By refining Selberg's method, we study the large values of 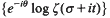 as
as