Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-30T22:55:13.187Z Has data issue: false hasContentIssue false
  • English
  • Français

THE KAKEYA SET AND MAXIMAL CONJECTURES FOR ALGEBRAIC VARIETIES OVER FINITE FIELDS

Part of: Harmonic analysis in several variables Finite geometry and special incidence structures Arithmetic algebraic geometry

Published online by Cambridge University Press:  10 December 2009

Jordan S. Ellenberg ,
Richard Oberlin  and
Terence Tao
Jordan S. Ellenberg
Affiliation:
Department of Mathematics, University of Wisconsin, Madison WI 53706, U.S.A. (email: [email protected])
Richard Oberlin
Affiliation:
UCLA Department of Mathematics, Los Angeles, CA 90095-1555, U.S.A. (email: [email protected])
Terence Tao
Affiliation:
UCLA Department of Mathematics, Los Angeles, CA 90095-1555, U.S.A. (email: [email protected])
Get access

Abstract

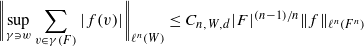Using the polynomial method of Dvir [On the size of Kakeya sets in finite fields. Preprint], we establish optimal estimates for Kakeya sets and Kakeya maximal functions associated to algebraic varieties W over finite fields F. For instance, given an (n−1)-dimensional projective variety W⊂¶n(F), we establish the Kakeya maximal estimate for all functions f:Fn→R and d≥1, where for each w∈W, the supremum is over all irreducible algebraic curves in Fn of degree at most d that pass through w but do not lie in W, and with Cn,W,d depending only on n,d and the degree of W; the special case when W is the hyperplane at infinity in particular establishes the Kakeya maximal function conjecture in finite fields, which in turn strengthens the results of Dvir.

MSC classification

Secondary: 42B25: Maximal functions, Littlewood-Paley theory 11G25: Varieties over finite and local fields 51E20: Combinatorial structures in finite projective spaces
Type
Research Article
Information
Mathematika , Volume 56 , Issue 1 , January 2010 , pp. 1 - 25
Copyright
Copyright © University College London 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Bergh, J. and Löfström, J., Interpolation Spaces: An Introduction, Springer (Berlin, 1976).CrossRefGoogle Scholar
[2]Bourgain, J., Besicovitch-type maximal operators and applications to Fourier analysis. Geom. Funct. Anal. 22 (1991), 147–187.CrossRefGoogle Scholar
[3]Bueti, J., An incidence bound for k-planes in F n and a planar variant of the Kakeya maximal function. Preprint.Google Scholar
[4]Calderón, A. and Zygmund, A., On singular integrals. Amer. J. Math. 78 (1956), 289–309.CrossRefGoogle Scholar
[5]Dvir, Z., On the size of Kakeya sets in finite fields. Preprint.Google Scholar
[6]Dvir, Z., Kopparty, S., Saraf, S. and Sudan, M., Extensions to the method of multiplicities, with applications to Kakeya sets and mergers. Preprint.Google Scholar
[7]Dvir, Z. and Wigderson, A., Kakeya sets, new mergers, and old extractors. Proceedings of the 49th Annual IEEE Symposium on Foundations of Computer Science, IEEE Computer Society (2008).CrossRefGoogle Scholar
[8]Hartshorne, R., Algebraic Geometry (Graduate Texts in Mathematics 52), Springer (New York, 1977).CrossRefGoogle Scholar
[9]Kleiman, S. L., Les théorèmes du finitude pour le foncteur de Picard. In Théorie des intersections et théorème de Riemann–Roch (SGA6), expose XIII (Lecture Notes in Mathematics 225), Springer (Berlin, 1971), 616–666.CrossRefGoogle Scholar
[10]Li, L., On the size of Nikodym sets in finite fields. Preprint.Google Scholar
[11]Mockenhaupt, G. and Tao, T., Kakeya and restriction phenomena for finite fields. Duke Math. J. 121 (2004), 35–74.CrossRefGoogle Scholar
[12]Pisier, G., Factorization of operators through L p,∞ or L p,1 and noncommutative generalizations. Math. Ann. 276 (1986), 105–136.CrossRefGoogle Scholar
[13]Saraf, S. and Sudan, M., Improved lower bound on the size of Kakeya sets over finite fields. Preprint.Google Scholar
[14]Serre, J. P., Local Fields (Graduate Texts in Mathematics 67), Springer (New York, 1979).CrossRefGoogle Scholar
[15]Stein, E., Limits of sequences of operators. Ann. of Math. (2) 74 (1961), 140–170.CrossRefGoogle Scholar
[16]Tao, T., The Bochner–Riesz conjecture implies the Restriction conjecture. Duke Math J. 96 (1999), 363–376.CrossRefGoogle Scholar
[17]Wolff, T., Recent work connected with the Kakeya problem. In Prospects in Mathematics (Princeton, NJ, 1996), American Mathematical Society (Providence, RI, 1999), 129–162.Google Scholar