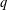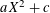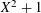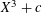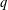Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Benedetto, Robert
Ingram, Patrick
Jones, Rafe
Manes, Michelle
Silverman, Joseph
and
Tucker, Thomas
2019.
Current trends and open problems in arithmetic dynamics.
Bulletin of the American Mathematical Society,
Vol. 56,
Issue. 4,
p.
611.
Bridy, Andrew
and
Garton, Derek
2020.
The Cycle Structure of Unicritical Polynomials.
International Mathematics Research Notices,
Vol. 2020,
Issue. 23,
p.
9120.
Ren, Rufei
2020.
Iteration of polynomials AX + C over finite fields.
Journal of Number Theory,
Vol. 214,
Issue. ,
p.
326.
Juul, Jamie
2021.
The Image Size of Iterated Rational Maps over Finite Fields.
International Mathematics Research Notices,
Vol. 2021,
Issue. 5,
p.
3362.
Hutz, Benjamin
and
Patel, Teerth
2022.
Periodic points and tail lengths of split polynomial maps modulo primes.
Involve, a Journal of Mathematics,
Vol. 15,
Issue. 2,
p.
185.
Mans, Bernard
Sha, Min
Shparlinski, Igor
and
Sutantyo, Daniel
2023.
Functional graphs of families of quadratic polynomials.
Mathematics of Computation,
Vol. 92,
Issue. 343,
p.
2307.
Andersen, Aaron
and
Garton, Derek
2024.
Preperiodic points of polynomial dynamical systems over finite fields.
International Journal of Number Theory,
Vol. 20,
Issue. 09,
p.
2307.