Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-22T20:11:08.876Z Has data issue: false hasContentIssue false
  • English
  • Français

INTEGRAL MONODROMY GROUPS OF KLOOSTERMAN SHEAVES

Part of: Linear algebraic groups and related topics Exponential sums and character sums Families, fibrations

Published online by Cambridge University Press:  08 June 2018

Corentin Perret-Gentil
Corentin Perret-Gentil*
Affiliation:
Department of Mathematics, ETH Zürich, Switzerland
Get access

Abstract

We show that integral monodromy groups of Kloosterman 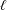$\ell$-adic sheaves of rank 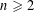$n\geqslant 2$ on 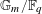$\mathbb{G}_{m}/\mathbb{F}_{q}$ are as large as possible when the characteristic 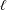$\ell$ is large enough, depending only on the rank. This variant of Katz’s results over 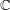$\mathbb{C}$ was known by works of Gabber, Larsen, Nori and Hall under restrictions such as 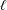$\ell$ large enough depending on 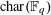$\operatorname{char}(\mathbb{F}_{q})$ with an ineffective constant, which is unsuitable for applications. We use the theory of finite groups of Lie type to extend Katz’s ideas, in particular the classification of maximal subgroups of Aschbacher and Kleidman–Liebeck. These results will apply to study hyper-Kloosterman sums and their reductions in forthcoming work.

MSC classification

Primary: 11L05: Gauss and Kloosterman sums; generalizations 14D05: Structure of families (Picard-Lefschetz, monodromy, etc.) 20G40: Linear algebraic groups over finite fields
Type
Research Article
Information
Mathematika , Volume 64 , Issue 3 , 2018 , pp. 652 - 678
Copyright
Copyright © University College London 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

Current address: Centre de recherches mathématiques, Université de Montréal, Case postale 6128, Montréal QC H3C 3J7, Canada [email protected]

References

Aschbacher, M., On the maximal subgroups of the finite classical groups. Invent. Math. 76(3) 1984, 469–514.Google Scholar
Carter, R. W., Simple Groups of Lie Type, John Wiley & Sons (London, New York, Sydney, Toronto, 1972).Google Scholar
Deligne, P., La conjecture de Weil. I. Publ. Math. Inst. Hautes Études Sci. 43(1) 1974, 273–307.Google Scholar
Deligne, P., Cohomologie Étale, Séminaire de Géométrie Algébrique du Bois-Marie SGA $\mathit{4}\frac{\mathit{1}}{\mathit{2}}$ (Lecture Notes in Mathematics 569), Springer (Berlin, Heidelberg, 1977).Google Scholar
Deligne, P., La conjecture de Weil. II. Publ. Math. Inst. Hautes Études Sci. 52(1) 1980, 137–252.Google Scholar
Fisher, B., Kloosterman sums as algebraic integers. Math. Ann. 301(1) 1995, 485–505.Google Scholar
Fu, L., Calculation of ℓ-adic local Fourier transformations. Manuscripta Math. 133(3–4) 2010, 409–464.Google Scholar
Fulton, W. and Harris, J., Representation Theory (Graduate Texts in Mathematics 129 ), Springer (New York, 1991).Google Scholar
Gorenstein, D., Finite Simple Groups: An Introduction to their Classification (University Series in Mathematics), Springer (New York, 1982).Google Scholar
Gorenstein, D., Lyons, R. and Solomon, R., The Classification of the Finite Simple Groups (Mathematical Surveys and Monographs 40 ), American Mathematical Society (1994).Google Scholar
Gow, R. and Tamburini, M. C., Generation of SL(n, p) by two Jordan block matrices. Boll. dell’Unione Mat. Ital. 7(6A) 1992, 346–357.Google Scholar
Hall, C., Big symplectic or orthogonal monodromy modulo ℓ . Duke Math. J. 141(1) 2008, 179–203.Google Scholar
Humphreys, J. E., Introduction to Lie Algebras and Representation Theory (Graduate Texts in Mathematics 9 ), Springer (New York, 1980).Google Scholar
Iwaniec, H. and Kowalski, E., Analytic Number Theory (Colloquium Publications), American Mathematical Society (Providence, RI, 2004).Google Scholar
Kantor, W. M. and Lubotzky, A., The probability of generating a finite classical group. Geom. Dedicata 36(1) 1990, 67–87.Google Scholar
Katz, N. M., Gauss Sums, Kloosterman Sums, and Monodromy Groups (Annals of Mathematics Studies 116 ), Princeton University Press (Princeton, NJ, 1988).Google Scholar
Katz, N. M., Exponential Sums and Differential Equations (Annals of Mathematics Studies 124 ), Princeton University Press (Princeton, NJ, 1990).Google Scholar
Katz, N. M., Report on the irreducibility of L-functions. In Number Theory, Analysis and Geometry, (eds Goldfeld, D., Jorgenson, J., Jones, P., Ramakrishnan, D., Ribet, K. and Tate, J.), Springer (New York, 2012), 321–353.Google Scholar
Katz, N. M. and Sarnak, P., Random Matrices, Frobenius Eigenvalues and Monodromy (Colloquium Publications 45 ), American Mathematical Society (Providence, RI, 1991).Google Scholar
Kleidman, P. B. and Liebeck, M. W., The Subgroup Structure of the Finite Classical Groups (London Mathematical Society Lecture Notes 129 ), Cambridge University Press (Cambridge, 1990).Google Scholar
Kloosterman, H., On the representation of numbers in the form ax 2 + by 2 + cz 2 + dt 2 . Acta Math. 49(3) 1927, 407–464.Google Scholar
Kowalski, E., On the rank of quadratic twists of elliptic curves over function fields. Int. J. Number Theory 2(2) 2006, 267–288.Google Scholar
Kowalski, E., The large sieve, monodromy and zeta functions of curves. J. Reine Angew. Math. 601 2006, 29–69.Google Scholar
Kowalski, E., Weil numbers generated by other Weil numbers and torsion field of abelian varieties. J. Lond. Math. Soc. (2) 74(2) 2006, 273–288.Google Scholar
Kowalski, E., The Large Sieve and its Applications: Arithmetic Geometry, Random Walks and Discrete Groups (Cambridge Tracts in Mathematics 175 ), Cambridge University Press (Cambridge, 2008).Google Scholar
Kowalski, E., Michel, P. and Sawin, W., Bilinear forms with Kloosterman sums and applications. Ann. of Math. (2) 186(2) 2017, 413–500.Google Scholar
Landazuri, V. and Seitz, G. M., On the minimal degrees of projective representations of the finite Chevalley groups. J. Algebra 32(2) 1974, 418–443.Google Scholar
Larsen, M., Maximality of Galois actions for compatible systems. Duke Math. J. 80(3) 1995, 601–630.Google Scholar
Larsen, M. and Pink, R., Finite subgroups of algebraic groups. J. Amer. Math. Soc. 24(4) 2011, 1105–1158.Google Scholar
Liebeck, M. W., On the orders of maximal subgroups of the finite classical groups. Proc. Lond. Math. Soc. (3) 3(3) 1985, 426–446.Google Scholar
Liebeck, M. W. and Seitz, G. M., On the subgroup structure of classical groups. Invent. Math. 134(2) 1998, 427–453.Google Scholar
Malle, G. and Testerman, D., Linear Algebraic Groups and Finite Groups of Lie Type (Cambridge Studies in Advanced Mathematics 133 ), Cambridge University Press (Cambridge, 2011).Google Scholar
Nori, M. V., On subgroups of GL n (F p ). Invent. Math. 88(2) 1987, 257–275.Google Scholar
Perret-Gentil, C., Probabilistic aspects of short sums of trace functions over finite fields. PhD Thesis, ETH Zürich, 2016.Google Scholar
Robinson, D., A Course in the Theory of Groups (Graduate Texts in Mathematics 80 ), Springer (1996).Google Scholar
Saxl, J. and Seitz, G. M., Subgroups of algebraic groups containing regular unipotent elements. J. Lond. Math. Soc. (2) 55(02) 1997, 370–386.Google Scholar
Seitz, G. M. and Testerman, D. M., Extending morphisms from finite to algebraic groups. J. Algebra 131(2) 1990, 559–574.Google Scholar
Serre, J.-P., Abelian ℓ-Adic Representations and Elliptic Curves (Research Notes in Mathematics 7 ), Addison-Wesley (Reading, MA, 1989).Google Scholar
Suprunenko, I. D., Irreducible representations of simple algebraic groups containing matrices with big Jordan blocks. Proc. Lond. Math. Soc. (3) 3(2) 1995, 281–332.Google Scholar
Testerman, D. and Zalesski, A., Irreducibility in algebraic groups and regular unipotent elements. Proc. Amer. Math. Soc. 141(1) 2013, 13–28.Google Scholar
Wagner, A., The faithful linear representations of least degree of S n and A n over a field of odd characteristics. Math. Z. 154 1977, 103–114.Google Scholar
Wan, D., Minimal polynomials and distinctness of Kloosterman sums. Finite Fields Appl. 1(2) 1995, 189–203.Google Scholar
Washington, L. C., Introduction to Cyclotomic Fields (Graduate Texts in Mathematics 83 ), Springer (New York, 1997).Google Scholar