Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-23T12:56:30.418Z Has data issue: false hasContentIssue false
  • English
  • Français

Inequalities between mixed volumes of convex sets

Published online by Cambridge University Press:  26 February 2010

G. C. Shephard
G. C. Shephard
Affiliation:
The University, Birmingham, 15.
Get access

Extract

Let K = {K1, K2, …, Kp} be a system of p bounded closed convex sets in affine space An of n dimensions. If λ1, λ2,…, λp are any p real numbers, we use λ1K1+λ2K2+…λpKp to denote the bounded closed convex set consisting of all the points

The n-dimensional content or volume of this set is a homogeneous polynomial of degree n in the parameters λi, that is

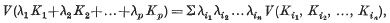
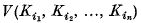where the summation is over all sets of suffixes 1 £ij, £p, for 1 £j £ n. Further the coefficients may be chosen to be positive and symmetric in their arguments 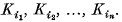These coefficients, which are 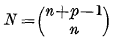in number, are called the mixed volumes of the convex sets.

Type
Research Article
Information
Mathematika , Volume 7 , Issue 2 , December 1960 , pp. 125 - 138
Copyright
Copyright © University College London 1960

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

page 125 note † For a proof of this result and discussions of the properties of mixed volumes see: Bonnesen, T. and Fenchel, W., Theorie der konvexen Körper (New York, 1948)Google Scholar, §7 et seq.; Eggleston, H. G., Convexity (Cambridge 1958)CrossRefGoogle Scholar, Chapter 5; Busemann, H., Convex surfaces (New York 1958), Chapter 2.Google Scholar

page 125 note ‡ Macbeath, A. M., “A compactness theorem for affine equivalence-classes of convex regions”, Can. J. of Math., 3 (1951), 54–61.CrossRefGoogle Scholar

page 125 note § Heine, R., “Der Wertvorrat der gemischten Inhälte von zwei, drei und vier obenen Eibereichen”, Math. Annalen, 115 (1937), 115–129.CrossRefGoogle Scholar

page126 note † Throughout this paper every convex set will be understood to be closed and bounded.

page127 note † A. M. Macbeath, loc. cit. p. 54. The metric used by Eggleston (loc. cit. pp. 59–60) is equivalent to this.

page130 note † A. M. Macbeath, loc. cit., p. 55.

page130 note ‡ H. G. Eggleston, loc. cit., Theorem 32.

page131 note † H. G. Eggleston, loc. cit., p. 87, Cor. to Theorem 42.

page132 note † H. Busemann, loc. cit., pp. 48–60.

page132 note ‡ It is clear that these cannot be deduced from 2.1 without the assumption 2.2, since, taking n = 3, p = 2, the values

satisfy 2.1, but not 2.3. In fact it is not difficult to see that when p = 2, if we interpret the mixed volumes as coordinates in projective space PN−1 as in the last section, equations 2.3 define the closure of the point set given by 2.1 and 2.2.

page132 note § Cf. R. Heine, loc. cit., p. 116.

page133 note † T. Bonnesen and W. Fenchel, loc. cit., p. 40.